При исследовании процессов в сложных электрических цепях часто интересуются током, напряжением и мощностью только одной ветви. Однако отдельные ветви могут быть выделены из сложной цепи не только для исследования процессов именно в этих ветвях, но и для установления связи, например, между одной частью цепи с источниками электрической энергии и другой с приемниками. Во всех этих случаях выделяют ветвь, присоединенную к сложной цепи в двух точках (двумя выводами). Часть электрической цепи произвольной конфигурации с двумя выделенными выводами или полюсами называется двухполюсником.
Двухполюсники, содержащие источники электрической энергии, называются активными, а двухполюсники, не содержащие источников электрической энергии, — пассивными. Всякий пассивный двухполюсник является потребителем электрической энергии и характеризуется одной величиной — сопротивлением ,. Поэтому на эквивалентной схеме пассивный двухполюсник может быть представлен одним резистивным элементом с сопротивлением называемым входным сопротивлением пассивного двухполюсника.
Если известна схема пассивного двухполюсника, то для определения входного сопротивления нужно тем или иным способом ее «свернуть» относительно двух заданных выводов.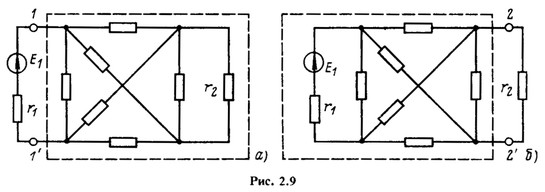
Рассмотрим, например, схему на рис. 2.9, а. Если выделить в этой схеме ветвь с источником ЭДС Е₁ и сопротивлением r₁, то остальную часть схемы (обведенную штриховой линией) можно рассматривать относительно выводов 1-1′ как пассивный двухполюсник (без источников энергии). Часть той же схемы относительно выводов 2-2′ ветви с сопротивлением r₂ (рис. 2.9, б) можно рассматривать как активный двухполюсник (обведен штриховой линией).
В дальнейшем все активные двухполюсники (рис. 2.10, а) будем обозначать прямоугольниками с буквой А (активный), а пассивные (рис. 2.10, б) — прямоугольниками с буквой П (пассивный).
Относительно выводов а и b остальная часть схемы на рис. 2.8 является активным двухполюсником и поэтому обозначена буквой А.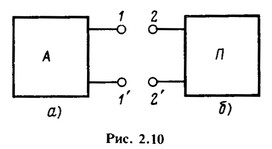
Если в электрической цепи выделено более двух выводов, то соответствующий участок цепи называется многополюсником, например многолучевая звезда и эквивалентный многоугольник на рис. 1.29, а и б с выводами 1, 2, 3, …, h, …, n, в частном случае трехлучевая звезда и эквивалентный треугольник, т. е. трехполюсники, с четырьмя или двумя парами выводов, как на рис. 2.3, а и б, т. е. четырехполюсник.