Входные и взаимные проводимости, коэффициенты передачи

Пользуясь принципом наложения, напишем уравнение для тока в любой ветви, например h, линейной электрической цепи в виде

где — частичный ток в ветви h, обусловленный действием ЭДС .
В этом уравнении, составленном согласно указаниям в разделе ток в отличие от (1.49) обозначает ток ветви h, a E₁, Е₂ и т. д. — ЭДС соответственно в первой, второй и так далее ветвях, при этом, если положительное направление для тока h выбрано совпадающим с направлением ЭДС , то но составляющие токов в той же ветви вида создаваемые ЭДС других ветвей, могут быть и отрицательными.
В (2.5) множители при ЭДС имеют размерность проводимости. Каждый из множителей с двумя одинаковыми индексами вида называется входной проводимостью ветви h. Любой из множителей с двумя различными индексами называется взаимной проводимостью ветвей h и m. При заданных направлениях действия ЭДС и выбранном положительном направлении тока взаимные проводимости могут получиться либо положительными, либо отрицательными величинами.
Численные значения входных и взаимных проводимостей могут быть определены следующим путем. Приравняем в рассматриваемой схеме все ЭДС, кроме , нулю, при этом ток , откуда

Следовательно, входная проводимость любой ветви определяется отношением тока к ЭДС в этой ветви при равных нулю ЭДС в остальных ветвях.
Электродвижущая сила , включенная в ветвь h, вызывает в общем случае токи во всех ветвях и, в частности, в ветви m. Ток в ветви m определяется по уравнению, аналогичному (2.5), при равных нулю всех ЭДС, кроме , т. е.

, откуда

Отметим, что , как это непосредственно следует из свойства взаимности.
Таким образом, взаимная проводимость двух любых ветвей определяется отношением тока в одной ветви к ЭДС в другой при равных нулю ЭДС в остальных ветвях.

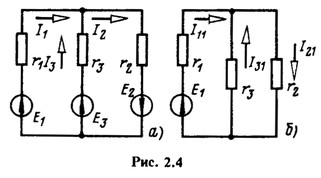Входные и взаимные проводимости можно рассчитать или определить экспериментально. Определение входных и взаимных проводимостей расчетом покажем на примере схемы рис. 2.4, а.
Приравняем ЭДС E₂ и E₃ нулю (рис. 2.4,6), при этом токи в ветвях

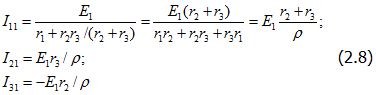
где

Из (2.8) определим:

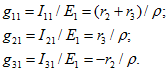
Аналогично рассчитываются входные и взаимные проводимости второй и третьей ветвей:

Если взаимные проводимости найдены, то легко определить токи во всех ветвях при любых значениях ЭДС. Так, для схемы рис. 2.4, а

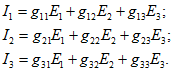
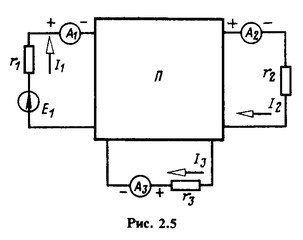Экспериментальное определение входных и взаимных проводимостей и сопротивлений рассмотрим на примере произвольной цепи, из которой предварительно исключены все источники ЭДС и источники тока (рис. 2.5). Три ветви этой цепи выделены, а остальная часть условно показана в виде прямоугольника. В каждую ветвь включен амперметр. Чтобы определить входную проводимость первой ветви g₃₁ и взаимные проводимости второй и первой g₂₁ и третьей и первой g₃₁ ветвей, надо включить в первую ветвь источник ЭДС Е₁. Измерив вольтметром напряжение U₁ = E₁ на выводах источника ЭДС и амперметрами токи I₁, I₂ и I₃ в трех ветвях, нетрудно вычислить входную и взаимные проводимости ветвей по формулам
Аналогично определяются входные и взаимные проводимости других ветвей.

Пример 2.2.
Определить входные и взаимные проводимости ветвей схемы рис. 2.6, а, если
Решение.
Для определения входной проводимости и взаимных проводимостей между первой и остальными ветвями положим Е₃ = E₅ = 0 (рис. 2.6, б). Затем можно задаться E₁ и найти все токи. Однако для данной схемы проще задать ток в ветви с сопротивлением r₄ или r₅, например I₅₁ = = 1 А, и найти необходимую ЭДС E₁ и токи в остальных ветвях.
Так как r₄ = r₅, то I₄₁ = I₅₁ и I₃₁ = — (I₅₁ + I₄₁) = — 2 А. На выводах элемента с сопротивлением r2 напряжение ; токи и ЭДС, при действии которой ток I₅₁ = 1 А, а остальные токи равны найденным значениям, .
Входная проводимость первой ветви .
Взаимные проводимости между первой и остальными ветвями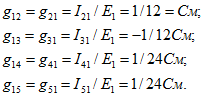

Аналогично определяются входные и взаимные проводимости остальных ветвей:

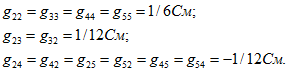
При определении проводимостей следует включить ЭДС Е2 в ветвь 2, направленную так же, как и ток I₂, а при определении ЭДС E₄ в ветвь 4.

Пример 2.3.
В условиях предыдущей задачи (см. пример 2.2) определить токи во всех ветвях, если ЭДС Е₁ = 24 В, E₃ = 12 В и E₅ = 24 В.
Решение.
Зная входные и взаимные проводимости ветвей, легко определить в них токи, пользуясь принципом наложения:

и т.д.

Если кроме источников ЭДС схема содержит и источники тока, то по принципу наложения к частичным токам, обусловленным действием источников ЭДС, добавятся частичные токи, обусловленные каждым из источников тока:

При определении входных и взаимных проводимостей все токи следует считать равными нулю (источники тока не действуют), а ветви с источниками тока разорвать (идеальные источники тока). При расчете коэффициентов передачи следует считать все ЭДС .

Пример 2.4.
Составить зависимость при r₁ = r₂ = r₃ = 2 Ом в схеме рис. 2.7, а.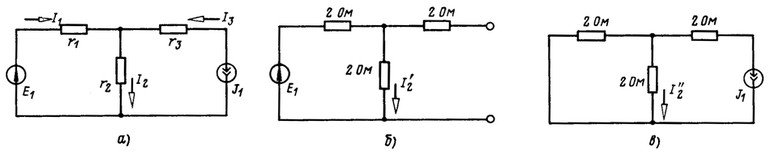

Решение.
Ток Проводимость определяется расчетом режима в схеме рис. 2.7, б. Ток . Коэффициент определяется расчетом режима в схеме рис. 2.7, в. Ток