Передача энергии от активного двухполюсника к пассивному
Для исследования передачи энергии от активного двухполюсника к пассивному вернемся к эквивалентной схеме, показанной на рис. 2.14, д, и будем считать, что rвх — входное сопротивление активного двухполюсника (источника энергии) и Еэк = Uх — эквивалентная ЭДС остаются постоянными, а r — входное сопротивление пассивного двухполюсника может принимать любое значение.
Прежде всего установим соотношение между сопротивлениями rвх и r, при выполнении которого мощность пассивного двухполюсника максимальна.
Мощность пассивного двухполюсника определяется выражениями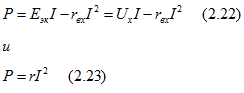
где ![]() —мощность, развиваемая эквивалентным активным двухполюсником;
—мощность, развиваемая эквивалентным активным двухполюсником; ![]() -мощность потерь в этом двухполюснике (в сопротивлении rвх).
-мощность потерь в этом двухполюснике (в сопротивлении rвх).
Для определения тока I, при котором мощность Р максимальна, найдем производную от Р по I из уравнения (2.22) и приравняем ее нулю:![]()
откуда искомый ток ![]() [уравнением (2.23) пользоваться нельзя, так как его правая часть содержит две переменные: r и I].
[уравнением (2.23) пользоваться нельзя, так как его правая часть содержит две переменные: r и I].
В общем случае (рис. 2.14, д) ток ![]() . Значит, мощность максимальна при
. Значит, мощность максимальна при
![]()
т. е. при равенстве входных сопротивлений пассивного и активного двухполюсников.
По (2.23) при r = rвх мощность
![]()
Отношение мощности Р пассивного двухполюсника к мощности ![]() , развиваемой эквивалентным активным
, развиваемой эквивалентным активным
двухполюсником, называется КПД эквивалентного активного двухполюсника:
![]()
Из (2.25) следует, что при максимальной мощности пассивного двухполюсника КПД равен 0,5. Более высокие значения КПД будут при ![]() .
.
КПД реального активного двухполюсника равен КПД эквивалентного только при выполнении определенного условия. Если при отключении пассивного двухполюсника от реального активного в ветвях последнего не будет токов и потерь, так же как и в эквивалентной схеме на рис. 2.14, д, то КПД реального и эквивалентного активных двухполюсников равны. При невыполнении этого условия КПД реального активного двухполюсника меньше КПД эквивалентного двухполюсника.
Полученные результаты применим, например, для характеристики режима линии передачи электрической энергии небольшой длины, у которой утечкой тока (между проводами) можно пренебречь.
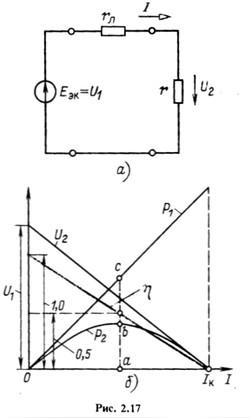
Если в начале линии передачи напряжение U1 поддерживается неизменным (рис. 2.17, а), то линию можно представить в виде последовательного соединения активного двухполюсника с источником ЭДС ![]() (без внутреннего сопротивления), резистивного элемента, учитывающего сопротивление проводов rл, и пассивного двухполюсника — приемника с сопротивлением r (рис. 2.17, а). По (2.22) и (2.25) найдем мощность Р2 приемника и КПД линии передачи:
(без внутреннего сопротивления), резистивного элемента, учитывающего сопротивление проводов rл, и пассивного двухполюсника — приемника с сопротивлением r (рис. 2.17, а). По (2.22) и (2.25) найдем мощность Р2 приемника и КПД линии передачи:
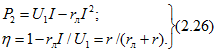
Мощность, развиваемая источником,
![]()
напряжение на выводах приемника
![]()
По полученным уравнениям на рис. 2.17,6 построены зависимости ![]() от тока I, полностью характеризующие режим линии.
от тока I, полностью характеризующие режим линии.
При ![]() (холостой ход линии) ток I = 0 (на рис. 2.17, б -точка в начале координат), при
(холостой ход линии) ток I = 0 (на рис. 2.17, б -точка в начале координат), при ![]() ток определяется отрезком Оa и при r = 0 (короткое замыкание линии) значение тока максимально и равно
ток определяется отрезком Оa и при r = 0 (короткое замыкание линии) значение тока максимально и равно ![]() . Кроме того, при
. Кроме того, при ![]() мощность
мощность ![]() , определяемая отрезком ас, равна удвоенной мощности приемника (ас = 2ab = 2bc), и КПД
, определяемая отрезком ас, равна удвоенной мощности приемника (ас = 2ab = 2bc), и КПД ![]() .
.
По эквивалентной схеме (рис. 2.17, а) установим еще связь между потерями в проводах линии (в сопротивлении rл) и мощностью приемника Р2:
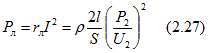
где l — длина линии; S — сечение каждого провода.
Из (2.27), в частности, следует, что при Р2 = const с повышением напряжения U2 требуется меньшее значение тока I и, следовательно, уменьшаются потери в проводах, что в свою очередь позволяет уменьшить сечение проводов. Конечно, при этом надо усилить изоляцию проводов линии.
В случае передачи по линии электрической энергии при большой мощности стремятся получить возможно больший КПД, для чего необходимо, как непосредственно следует из (2.26), иметь ![]() . При передаче сигналов по линии связи стремятся получить максимальную мощность в приемнике, что приводит к низкому значению КПД.
. При передаче сигналов по линии связи стремятся получить максимальную мощность в приемнике, что приводит к низкому значению КПД.
Первые опыты передачи электрической энергии при постоянном токе осуществил русский инженер Ф. А. Пироцкий. В 1874 г. вблизи г. Петербурга Ф. А. Пироцкий создал линию передачи энергии при мощности около 6 л. с. на расстояние до 1 км. Затем он проводил опыты передачи электрической энергии по рельсам конно-железной дороги. На основании своих опытов Ф. А. Пироцкий установил, что можно передавать электрическую энергию при большой мощности на большие расстояния. В качестве источников энергии для первичных двигателей он предложил пользоваться энергией водных потоков. Теоретические основы передачи электрической энергии по линии разработал Д. А. Лачинов. В 1880 г. он опубликовал в первом номере журнала «Электричество» свой труд «Электромеханическая работа».
Опыты Ф. А. Пироцкого остались совершенно незамеченными. И лишь этим можно объяснить, что инициатором передачи электрической энергии считался Марсель Депре. В своем докладе в Парижской академии наук (1881 г.) он провозгласил тезис, установленный почти за год до этого Д. А. Лачиновым, а именно: повышая напряжение, можно передавать электрическую энергию при любой мощности на большое расстояние с минимальными потерями (2.27). В следующем году (1882 г.) Депре осуществил на постоянном токе передачу энергии при мощности в 2 л. с. на расстояние 57 км (при напряжении 1500 — 2000 В).
Электрические цепи постоянного тока
Пример расчета цепей постоянного тока
Элементы электрических цепей и схем
Схемы замещения источников энергии
Закон Ома для участка цепи с ЭДС
Баланс мощностей для простой неразветвленной цепи
Законы Кирхгофа и их применение
Топологические графы
Законы Кирхгофа в матричной форме
Метод узловых потенциалов
Метод контурных токов
Уравнения цепи в матричной форме
Расширенные узловые уравнения
Преобразования в линейных электрических схемах
Принцип наложения (суперпозиции)
Свойство взаимности
Входные и взаимные проводимости, коэффициенты передачи
Принцип компенсации. Зависимые источники
Общие замечания о двухполюсниках и многополюсниках
Линейные соотношения между напряжениями и токами
Теорема о взаимных приращениях токов и напряжений
Принцип эквивалентного генератора
Передача энергии от активного двухполюсника к пассивному