Свойство взаимности
Пользуясь методом контурных токов, установим еще одно важное свойство линейных электрических цепей — свойство взаимности, или, как его еще называют, принцип взаимности.
Сущность этого свойства заключается в следующем. Пусть в схеме произвольной конфигурации единственный источник ЭДС ![]() действует в ветви с сопротивлением
действует в ветви с сопротивлением ![]() в направлении от точки b к точке а (рис. 2.3, а) и создает в ветви с сопротивлением
в направлении от точки b к точке а (рис. 2.3, а) и создает в ветви с сопротивлением ![]() ток
ток ![]() направленный от точки d к точке с. Такой же единственный источник ЭДС
направленный от точки d к точке с. Такой же единственный источник ЭДС ![]() включенный в ветвь с сопротивлением
включенный в ветвь с сопротивлением ![]() и действующий в направлении от d к с (рис. 2.3,6), создаст в ветви с сопротивлением
и действующий в направлении от d к с (рис. 2.3,6), создаст в ветви с сопротивлением ![]() ток
ток ![]() , направленный от b к а и равный току
, направленный от b к а и равный току ![]() .
.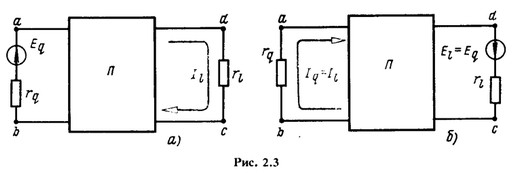
На рис. 2.3 изображены ветви ub и cd с сопротивлениями ![]() а остальная часть схемы, не содержащая источников энергии, условно показана в виде прямоугольника с буквой П (пассивная).
а остальная часть схемы, не содержащая источников энергии, условно показана в виде прямоугольника с буквой П (пассивная).
Для доказательства свойства взаимности обратимся к выражению (1.49), определяющему ток в любом контуре. Пусть ветвь cd является частью контура l а ветвь ab входит в состав другого контура q (рис. 2.3,а), и, как указано, других источников, кроме источника ЭДС ![]() эта цепь не содержит. Контуры выберем так, чтобы ветви ab и cd вошли каждая в один контур, соответственно q и l.
эта цепь не содержит. Контуры выберем так, чтобы ветви ab и cd вошли каждая в один контур, соответственно q и l.
Ток в контуре l, равный току ветви dc,
![]()
Если источник ЭДС ![]() переставить в ветвь cd контура l (рис. 2.3,6), та согласно (1.49) ток
переставить в ветвь cd контура l (рис. 2.3,6), та согласно (1.49) ток ![]() в контуре q, т. е. ток в ветви ab,
в контуре q, т. е. ток в ветви ab,![]()
Алгебраическое дополнение вида ![]() получается из определителя
получается из определителя ![]() путем вычеркивания в нем столбца l и строки q и умножения получаемого определителя на
путем вычеркивания в нем столбца l и строки q и умножения получаемого определителя на ![]() , а алгебраическое дополнение вида
, а алгебраическое дополнение вида ![]() — вычеркиванием столбца q и строки l и умножением получаемого определителя на
— вычеркиванием столбца q и строки l и умножением получаемого определителя на ![]() . Так как в контурных уравнениях общие сопротивления
. Так как в контурных уравнениях общие сопротивления ![]() равны друг другу, т. е.
равны друг другу, т. е. ![]() и т. д., то и
и т. д., то и ![]() (отличаются только тем, что строки
(отличаются только тем, что строки ![]() являются столбцами
являются столбцами ![]() и наоборот). Следовательно, при равенстве ЭДС
и наоборот). Следовательно, при равенстве ЭДС ![]() токи в ветвях cd (рис. 2.3, а) и ab (рис. 2.3,6) равны друг другу.
токи в ветвях cd (рис. 2.3, а) и ab (рис. 2.3,6) равны друг другу.
Отметим, что свойство взаимности справедливо не только для токов, но и для напряжений, и его можно также обосновать, пользуясь законами Кирхгофа или методом узловых потенциалов.
Электрические цепи постоянного тока
Пример расчета цепей постоянного тока
Элементы электрических цепей и схем
Схемы замещения источников энергии
Закон Ома для участка цепи с ЭДС
Баланс мощностей для простой неразветвленной цепи
Законы Кирхгофа и их применение
Топологические графы
Законы Кирхгофа в матричной форме
Метод узловых потенциалов
Метод контурных токов
Уравнения цепи в матричной форме
Расширенные узловые уравнения
Преобразования в линейных электрических схемах
Принцип наложения (суперпозиции)
Свойство взаимности
Входные и взаимные проводимости, коэффициенты передачи
Принцип компенсации. Зависимые источники
Общие замечания о двухполюсниках и многополюсниках
Линейные соотношения между напряжениями и токами
Теорема о взаимных приращениях токов и напряжений
Принцип эквивалентного генератора
Передача энергии от активного двухполюсника к пассивному