Расширенные узловые уравнения
При составлении расширенных узловых уравнений все ветви схемы разделим на два подмножества: g-ветви и r-ветви (рис. 1.26, а и б) — частные случаи обобщенной ветви (см. рис. 1.25).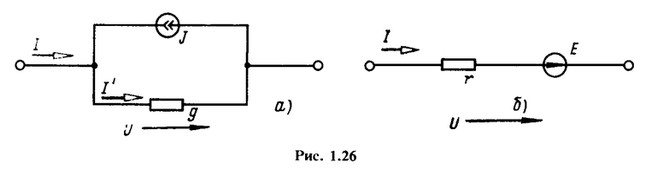
Для g-ветви компонентное уравнение
I = gU — J,
и в матричной форме для всего подмножества g-ветвей![]()
где g — диагональная матрица проводимостей g-ветвей. Ветвь с идеальным источником тока следует считать g-ветвью, у которой проводимость g = 0. Для r-ветви компонентное уравнение
U — rl — Е,
и в матричной форме для всего подмножества r-ветвей![]()
где r — диагональная матрица сопротивлений r-ветвей.
Ветвь с идеальным источником ЭДС следует считать r-ветвью, у которой сопротивление r = 0.
При составлении топологических уравнений по первому закону Кирхгофа AI = 0 выберем первые номера для g-ветвей. Поэтому запишем первое уравнение Кирхгофа в виде
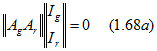
или
![]()
Напряжения ветвей связаны с потенциалами узлов матричным уравнением ( 1.40) ![]() или при выбранной нумерации ветвей
или при выбранной нумерации ветвей
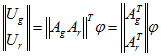
т.е.
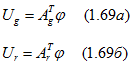
Заменив в (1.66) Ug по (1.69а) и в (1.68) 1в по (1.66), получим![]()
В (1.67) подставим Ur по (1.696) и получим![]()
Уравнения (1.70) и (1.71) определяют потенциалы узлов φ и токи r-ветвей Ir при заданной конфигурации схемы и значениях ее элементов g, J, r и Е. В (1.70) ![]() — узловая матрица проводимостей, но не всех ветвей, а только g-ветвей;
— узловая матрица проводимостей, но не всех ветвей, а только g-ветвей; ![]() — узловой ток.
— узловой ток.
Уравнения (1.70) и (1.71) можно объединить в матричное расширенное узловое уравнение:
![]()
Решение системы уравнений не требует перемножения матриц, снимает ограничения, которые необходимо учитывать при расчете режима цепи с применением метода узловых потенциалов, но количество совместно решаемых уравнений увеличивается на число r-ветвей.
Пример 1.4.
Составить матричное уравнение методом расширенных узловых уравнений для схемы по рис. 1.27 при параметрах r1 = 1 Ом, r2 = 2 Ом, r3 = 3 Ом, E4 = 4B, J1=4A.
Решение. 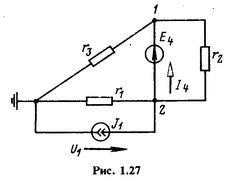
Схема состоит из трех g-ветвей: 1) с источником тока J1 и сопротивлением r1, т. е. с проводимостью g1 = 1 См; 2) с сопротивлением r2, т. е. с проводимостью g2 = 1/2 См; 3) с сопротивлением r3, т. е. с проводимостью g3 = 1/3 См, и одной r-ветви с ЭДС E4 и сопротивлением r4 = 0. При этом методом расширенных узловых уравнений определяются потенциалы узлов φ1 и φ2 и ток I4 в r-ветви. Последние две g-ветви можно было бы считать r-ветвями с ЭДС E2 = 0 и E3 = 0, но при этом число совместно решаемых уравнений увеличится (добавятся токи в сопротивлениях r2 и r3).
Составим матрицы, входящие в матричное уравнение (1.72). Квадратная матрица узловых проводимостей второго порядка (узлы 1 и 2)
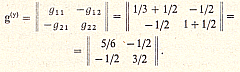
Матрица соединений g-ветвей (одна ветвь с током I4, который направлен к узлу 1)
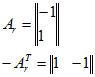
В r-ветви сопротивление равно нулю, т. е. к = 0. Матрица-столбец узловых токов (два узла) ![]() . Матрица-столбец ЭДС r-ветвей Е = 4 (одна ветвь).
. Матрица-столбец ЭДС r-ветвей Е = 4 (одна ветвь).
В результате получаем матричное уравнение (1.72)
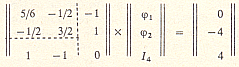
после решения которого находим ![]() . Остальные токи определяются по закону Ома и первому закону Кирхгофа после выбора их положительных направлений.
. Остальные токи определяются по закону Ома и первому закону Кирхгофа после выбора их положительных направлений.
После формирования матриц любого из рассмотренных выше общих методов расчет режима цепи сводится к задаче решения системы линейных алгебраических уравнений.
Электрические цепи постоянного тока
Пример расчета цепей постоянного тока
Элементы электрических цепей и схем
Схемы замещения источников энергии
Закон Ома для участка цепи с ЭДС
Баланс мощностей для простой неразветвленной цепи
Законы Кирхгофа и их применение
Топологические графы
Законы Кирхгофа в матричной форме
Метод узловых потенциалов
Метод контурных токов
Уравнения цепи в матричной форме
Расширенные узловые уравнения
Преобразования в линейных электрических схемах
Принцип наложения (суперпозиции)
Свойство взаимности
Входные и взаимные проводимости, коэффициенты передачи
Принцип компенсации. Зависимые источники
Общие замечания о двухполюсниках и многополюсниках
Линейные соотношения между напряжениями и токами
Теорема о взаимных приращениях токов и напряжений
Принцип эквивалентного генератора
Передача энергии от активного двухполюсника к пассивному