Трансформаторные подстанции высочайшего качества

В предыдущих разделах был дан анализ переходных процессов в неразветвленных цепях. Порядок анализа переходных процессов в разветвленных цепях рассмотрим на достаточно простом примере расчета тока в цепи рис. 14.24, чтобы нетрудно было проследить путь анализа и все его этапы. Далее будут даны необходимые пояснения.

1. Для цепи после коммутации составим систему дифференциальных уравнений по первому и второму законам Кирхгофа: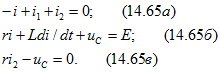

где . После подстановки в (14.65) и дифференцирования уравнений (14.65 6 и в) получим систему уравнений для трех неизвестных токов:

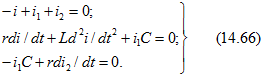
2. Независимые начальные условия — ток в индуктивном элементе и напряжение на емкостном элементе — неизвестны. Поэтому определим их из расчета режима цепи до коммутации с применением законов коммутации.
Считая, что до коммутации в левом контуре был установившийся режим, при остоянной ЭДС Е конденсатор был заряжен до напряжения , т. е. , а ток был равен нулю, т. е. . Это и есть независимые начальные условия.

3. Запишем искомую величину в виде суммы установившейся и свободной составляющих: .

4. Установившуюся составляющую найдем, рассчитав режим цепи постоянного тока (ЭДС в цепи постоянная) после коммутации.
В установившемся режиме после коммутации ток есть только во внешнем контуре, a .

5. Составим характеристическое уравнение и найдем его корни.
Из системы трех уравнений (14.66) с тремя неизвестными можно исключить токи и для полученного дифференциального уравнения записать характеристическое уравнение. Однако для определения корней можно составить главный определитель системы (14.66) и приравнять его к нулю:

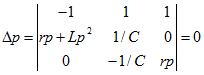
Рис. 14.24

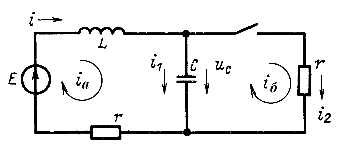
или
Корень р = 0 соответствует установившемуся режиму, который уже найден. Два других корня определяются из характеристического уравнения Они могут быть действительные разные , равные или комплексные сопряженные (действительная часть корней не может быть положительной, так как в рассматриваемых цепях переходные процессы затухают).

6. Запишем свободную составляющую с постоянными интегрирования, обращая внимание на вид корней (действительные различные, равные, комплексные сопряженные):

Далее для определенности будем предполагать случай действительных разных корней.

7. Искомое решение с двумя постоянными интегрирования

8. Для определения двух постоянных интегрирования запишем полученное решение и его производную для начального момента времени

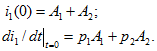
Это два алгебраических уравнения, из которых можно найти постоянные при известных значениях Начальное значение тока определим из системы дифференциальных уравнений цепи (14.65), записанной для момента t = 0:

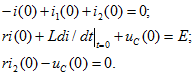
В этой системе алгебраических уравнений с тремя токами, производной тока и напряжением две величины и были уже найдены с применением законов коммутации. Следовательно, остальные три величины можно вычислить.
Для определения начального значения производной дифференцируем систему уравнений Кирхгофа (14.65) и подставляем t = 0:

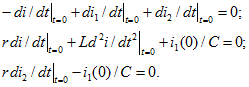
Это система трех алгебраических уравнений с тремя неизвестными , которые и можно вычислить. В рассматриваемой задаче достаточно найти
При трех корнях характеристического уравнения потребовалось бы еще раз продифференцировать уравнения Кирхгофа для определения третьего начального значения — второй производной искомой величины при t = 0, и т. д.

9. После определения постоянных остается подставить их в искомое решение, и расчет закончен.
Для определения других токов и напряжений не требуется заново выполнять все этапы расчета. Действительно,

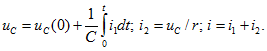
О системе дифференциальных уравнений.
Необходимое число уравнений, составляемых по первому и второму законам Кирхгофа, определяется так же, как и при расчете установившихся режимов в цепях постоянного и переменного токов. Независимые контуры выбираются по тем же правилам, что и для цепей постоянного и переменного токов.

Независимые начальные условия.
В цепи рис. 14.24 ЭДС Е постоянная. Если ЭДС синусоидальная , то ток до коммутации , т. e. и , напряжение , т. е.

Установившийся режим после коммутации.
При синусоидальной ЭДС в цепи рис. 14.24 ток , т .e. и аналогично .

Характеристическое уравнение дифференциального уравнения n-го порядка, как известно, составляется алгебраизацией соответствующего однородного уравнения. Например, у дифференциального уравнения тока

характеристическое уравнение

имеет n корней, среди которых могут быть действительные и комплексные сопряженные, различные и одинаковые. Степень называется порядком цепи. Так были получены характеристические уравнения цепей, рассмотренных в предыдущих разделах.
Однако, как указывалось выше, при анализе переходных процессов классическим методом в цепи, для которой составлена система уравнений Кирхгофа, можно получить характеристическое уравнение, составив главный определитель системы дифференциальных уравнений. Для понижения порядка определителя, при помощи которого находятся корни характеристического уравнения, можно записать уравнения цепи с контурными токами. Например, для цепи на рис. 14.24, выбрав контуры с токами , составим систему уравнений

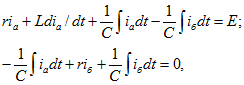
главный определитель которой

Уравнение имеет те же корни, что и характеристическое уравнение (14.68), т. е также является характеристическим.
Нетрудно заметить, что элементы определителя [в отличие от элементов ] — это собственные и общие комплексные сопротивления контуров той же самой цепи при замене оператором р: и т.д.
Таким образом, определитель (14.69) можно записать сразу без составления дифференциальных уравнений.
Составив комплексное входное сопротивление цепи для источника синусоидальной ЭДС (вместо источника ЭДС Е в цепи рис. 14.24) после замены оператором р получим

Как будет показано в разделе, уравнение

— это тоже характеристическое.
Источник ЭДС можно считать включенным в любую из ветвей цепи, т. е.

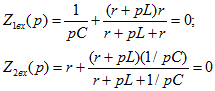
— это тоже характеристические уравнения.
Характеристическим является и уравнение

где — главный определитель системы, составленной методом узловых потенциалов с заменой оператором р. Например, для цепи на рис. 14.24 (с двумя узлами) определитель (первого порядка)

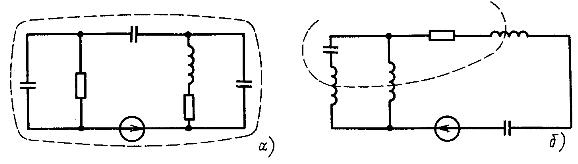
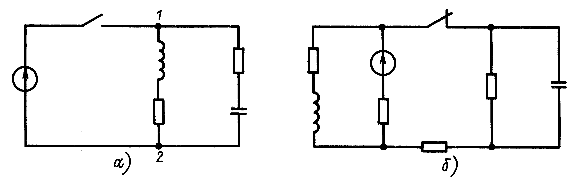
Число корней характеристического уравнения не может быть больше числа накопителей энергии в цепи после коммутации, т. е. числа ее индуктивных и емкостных элементов. Если схема замещения цепи не содержит особых контуров, состоящих только из емкостных элементов и источников ЭДС, и особых сечений, у которых в каждой ветви есть индуктивные элементы или источники тока, то число корней характеристического уравнения равно числу накопителей энергии. На рис. 14.25, а и б штриховой линией показаны особые контур и сечение. Число корней для цепи на рис. 14.25, а равно не 4, а 3 (один емкостной контур), для цепи на рис. 14.25,6 оно равно не 5, а 4 (одно индуктивное сечение).

Рис. 14.25

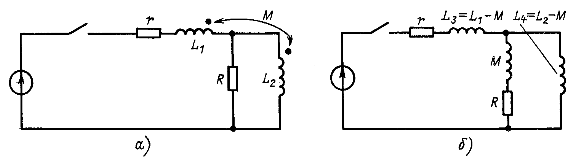
Наличие индуктивных связей не увеличивает числа корней характеристического уравнения. Например, для цепи на рис. 14.26, а запишем характеристическое уравнение, составив входное сопротивление для источника ЭДС после развязки индуктивной связи (рис. 14.26,6):

или

у которого два корня. Для цепи на рис. 14.26, а при отсутствии индуктивной связи характеристическое уравнение

или

т. е. тоже второго порядка (корни, конечно, другие).

Рис. 14.26

Корни характеристического уравнения определяются только топологией цепи после коммутации и значением ее параметров. В общем случае они одинаковы для любого из токов и напряжений цепи. Но следует обратить внимание на то, что в частных случаях, например в цепях на рис. 14.27, а и б, общее правило не выполняется. В цепи на рис. 14.27, а после замыкания рубильника задано напряжение между узлами 1 и 2. Поэтому на переходный процесс в каждой из ветвей с индуктивным и емкостным элементами не влияет вторая ветвь. Цепь на рис. 14.27, б после коммутации распадается на две отдельные цепи.

Рис. 14.27

Корни характеристического уравнения, как указывалось, имеют отрицательные действительные части (свободные составляющие процесса затухают). Это справедливо для всех цепей с потерями, в которых действуют только независимые источники ЭДС и тока. Следовательно, на комплексной плоскости точки, изображающие корни, располагаются на левой полуплоскости. В цепях с зависимыми источниками, например четырехполюсники — операционные усилители с обратной связью, возможно самовозбуждение. В этом случае характеристическое уравнение имеет хотя бы один корень (полюс передаточной функции) с положительной действительной частью, изображающая точка которого находится на правой полуплоскости (неустойчивость). Существуют критерии (Гурвица, Михайлова, Найквиста), дающие возможность судить об устойчивости без вычисления корней характеристического уравнения, т. е. полюсов.

Смотри пример по разделу