Трансформаторные подстанции высочайшего качества

Рассмотрим переходный процесс в цепи на рис. 14.31, а, у которой две катушки для упрощения вычислений с одинаковыми сопротивлениями и одинаковыми индуктивностями имеют индуктивную связь. Вторая катушка замкнута накоротко, а первая подключается к источнику постоянного напряжения U.
Токи в катушках связаны уравнениями Кирхгофа

Начальные условия нулевые, т. е. . Установившиеся значения токов .
Для определения корней характеристического уравнения составим главный определитель и приравняем его к нулю:

откуда находим два корня . Напомним, что учет индуктивной связи не увеличивает числа корней характеристического уравнения.
Токи

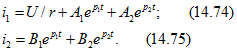
Чтобы вычислить постоянные кроме начального значения нужно найти .
Умножим (14.72) на L и (14.73) на М и вычтем (14.73) из (14.72) при t = 0:

откуда находим

При t = 0 из (14.74) следует

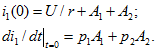
Рис. 14.31

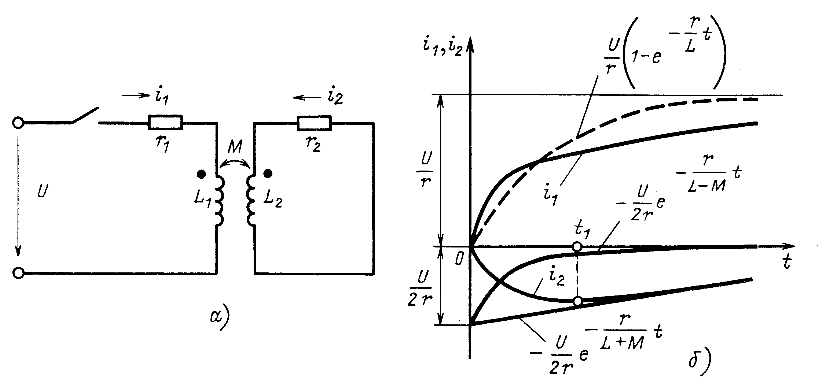
Отсюда определяем постоянные интегрирования . Аналогично находим и токи катушек

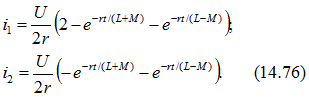
На рис. 14.31, б построены кривые изменения токов . Одна из свободных составляющих токов затухает медленнее, т. е. имеет большую постоянную времени, определяемую суммой индуктивности L и взаимной индуктивности М, а вторая затухает быстрее, так как ее постоянная времени определяется разностью L- М. Для сравнения на рис. 14.31, 6 показано, как изменялся бы ток первой катушки при ее включении, если бы вторая была разомкнута (штриховая кривая). В первые моменты после включения ток первой катушки увеличивается быстрее, чем он возрастал бы при разомкнутой второй катушке. В этом можно убедиться, подсчитав начальные значения производных в обоих случаях. При замкнутой второй катушке, как было найдено,

а при разомкнутой второй катушке (см. раздел)

В первом случае производная больше, поэтому ток растет быстрее.
Начиная с ток по абсолютному значению уменьшается и знак его производной изменяется на обратный. Кроме того, как показано на рис. 14.31, б, ток начиная с некоторого момента времени, растет медленнее, чем при разомкнутой второй катушке.
Попутно отметим, что, поскольку при включении токи катушек имеют противоположные направления, механические силы их взаимодействия стремятся оттолкнуть катушки друг от друга.
Рассмотрим энергетические соотношения.
Для этого умножим на обе части уравнения (14.72) и на обе части уравнения (14.73) и представим их в виде

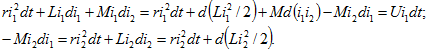
Подставив в предыдущее уравнение, получим

Проинтегрировав в пределах от 0 до t, будем иметь

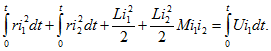
Отсюда следует, что получаемая от источника энергия преобразуется частично в тепло — джоулевы потери обеих катушек (первые два слагаемых левой части последнего равенства), а частично запасается в магнитном поле обеих катушек (три последних слагаемых левой части этого равенства). Так как знаки токов различны (рис. 14.31,6), то последний член отрицателен. Более подробный анализ показывает, однако, что знак суммы трех последних членов всегда положителен, так что за любой промежуток времени от 0 до t энергия источника частично переходит в тепло, а частично расходуется на увеличение энергии магнитного поля катушек.