Трансформаторные подстанции высочайшего качества

Для определения переходных процессов и установившихся режимов в линейных цепях при воздействии периодических импульсов напряжения или тока известно много методов. Некоторые из них основаны на суммировании токов или напряжений, созданных отдельными импульсами. В других методах для этой цели вводится периодическая импульсная реакция цепи. Третьи методы для той же цели вводят другую специальную характеристику цепи, так называемую эшелонную функцию.

Рассмотрим метод, основанный на непосредственном суммировании токов или напряжений, созданных отдельными импульсами, что реализуется учетом запаздывания последующих импульсов относительно предыдущих.
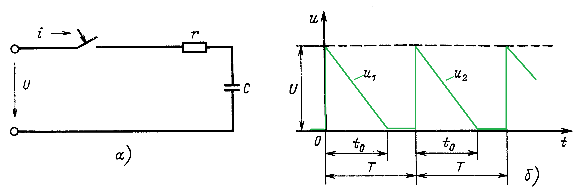
Поясним суть метода на примере расчета тока i в простейшей rС-цепи (рис. 14.50, а), которая в момент t = 0 подключается к источнику, создающему бесконечную последовательность импульсов напряжения, представленную на рис. 14.50,6.

Найдем сначала ток в цепи от воздействия первого импульса напряжения при и при . Переходная функция цепи находится известными методами:

Рис. 14.50

Применяя интеграл Дюамеля при , получаем

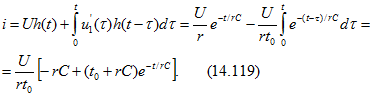
Для получаем

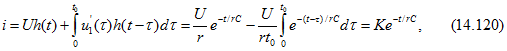
где

Перейдя к поставленной задаче, напишем формулу для тока i в промежутке времени, когда действует (n+1)-й импульс напряжения, т.е. при .
Как было указано выше, ток i представим в виде суммы токов, каждый из которых создается одним отдельно взятым импульсом напряжения. Первый импульс напряжения дает составляющую тока, определяемую формулой (14.120). Второй импульс запаздывает по отношению к первому на время Т, и ток от него равен . Для учета составляющей тока от третьего импульса напряжения нужно в (14.120) вместо t подставить t — 2T и т. д.
Составляющая тока от n-го импульса равна . Кроме того, следует учесть действие (n + 1)-го импульса напряжения, который на рассматриваемом промежутке времени еще не закончился. Созданную им составляющую тока найдем по формуле (14.119) с учетом запаздывания во времени nТ, т. е. вместо t подставим в (14.119) t — nТ.
Результирующий ток

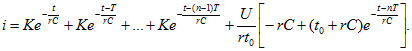
Суммируя первые n слагаемых, представляющих собой геометрическую прогрессию со знаменателем , для интервала получаем

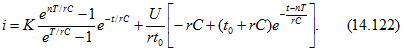
Далее запишем ток в промежутке времени, соответствующем (n + 1)-й паузе, т. е. при :

Для определения тока установившегося режима преобразуем (14.123) и (14.122), введя замену , где t‘ — время, отсчитываемое от начала действия (n + 1)-го импульса напряжения.
Для (14.122) получим

Для (14.123) будем иметь

Полагая в (14.124) и (14.125), что , находим установившийся ток. В течение действия импульса

в течение паузы

Если источник напряжения, начиная с момента t = 0, создает бесконечную последовательность импульсов без пауз, т. е. , то ток и для этого случая получим из (14.119), (14.120), (14.121), (14.122) и (14.126), положив в них .
При более сложной форме напряжения источника иногда целесообразнее рассматривать его как наложение импульсов на некоторое постоянное или какое-либо иное напряжение.