Электрические цепи постоянного тока

Электрическим током называют упорядоченное движение электрических зарядов. Направлением электрического тока условились считать направление движения положительных зарядов.

Можно указать на ряд факторов, способных вызывать упорядоченное движение зарядов. Так, под действием электрических (кулоновских) сил положительные заряды движутся в направлении силовых линий поля, отрицательные заряды — в противоположном направлении. Движение зарядов может происходить и под действием неэлектрических сил (например, магнитных), а также при диффузии или в химических реакциях.
Постоянный ток используется в процессе электролиза (гальванопластика — получение легко отделяющихся точных металлических копий, гальваностегия — нанесение металлических покрытий из одних металлов на изделия из других металлов), на городском транспорте (электропоезда, трамваи, троллейбусы), в осветительных приборах, в устройствах автоматики, электроники и вычислительной техники.
Если ток постоянный, то отсутствует явление самоиндукции и напряжение на катушке индуктивности равно нулю,
, так как i = const
Если рассматривать конденсатор как идеальную емкость, то в цепи постоянного тока эта ветвь равносильна разомкнутой.

Постоянный ток через емкость не проходит.

Таким образом, в цепи постоянного тока остаются только источники ЭДС или тока — активные элементы и приемники резисторы — пассивные элементы.
Простыми цепями постоянного тока называются цепи с одним источником при последовательном, параллельном и смешанном соединении приемников.

Последовательное соединение приемников

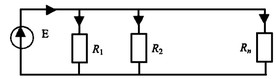
При параллельном соединении приемников напряжение на всех приемниках одинаково.
По закону Ома токи в каждой ветви:

По первому закону Кирхгофа общий ток

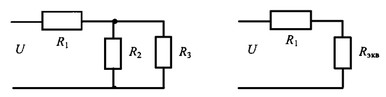
Смешанное соединение — комбинация первых двух соединений, где параллельное соединение может быть преобразовано к последовательному.

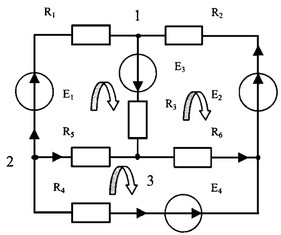
Сложной электрической цепью называется цепь, содержащая несколько источников и которую нельзя свернуть до простой цепи последовательного или параллельного соединения.
Расчет таких цепей ведется по уравнениям Кирхгофа.
Для их составления необходимо задать условные направления токов в ветвях (номер введем в соответствии с порядковым номером сопротивлений).
По первому закону Кирхгофа составляются уравнения для каждого из независимых узлов (для данной схемы таких узлов 3).

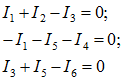
Выбираются направления обхода в каждом из независимых контуров и составляются уравнения по второму закону Кирхгофа — сумма падений напряжений на пассивных элементах замкнутого контура электрической цепи равна алгебраической сумме источников ЭДС в данном контуре:

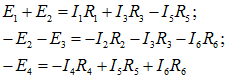
Для нахождения решения необходимо любым математическим способом решить полученные шесть уравнений, что весьма сложно. Чтобы сократить число уравнений, используют метод контурных токов.
Для вывода уравнений по методу контурных токов в общем виде исключим из последних трех уравнений токи ветвей смежных контуров , заменив их выражениями, полученными из первых трех уравнений:

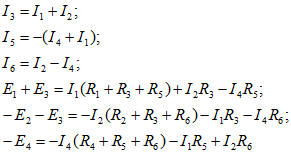
Введем обозначения контурных токов:
— ток первого контура;
— ток второго контура;
— ток третьего контура.
Для конкретизации и сокращения записи введем обозначения для контурных ЭДС, равных сумме ЭДС источников рассматриваемого контура:

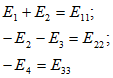
и соответственно суммы сопротивлений в каждом контуре через контурные сопротивления:

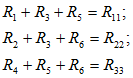
а сопротивления смежных ветвей как:

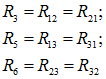
При принятых обозначениях система расчетных уравнений запишется в общем виде как:

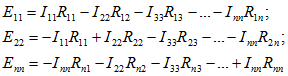
Мы видим, что при расчетах цепей с помощью правил Кирхгофа не обязательно знать разности потенциалов на определенных участках.

Практически правила Кирхгофа применяют следующим образом:
а) совершенно произвольно указывают стрелками направления токов на каждом из участков контура, а у источников тока отмечают знаки полюсов. Если после вычислений по правилам Кирхгофа сила тока на данном участке оказывается больше нуля, то это означает, что истинное направление тока совпало с направлением, указанным стрелкой; в противном случае ток направлен противоположно;
б) в выбранном произвольном контуре все его участки обходят в одном направлении — либо по часовой стрелке, либо в противоположном. При этом следует слагаемое IR считать положительным, если направление обхода контура совпадает с направлением тока. В противном случае это слагаемое отрицательно. Далее, если направление обхода контура выбрано от положительного полюса источника к отрицательному, то э. д. с. источника считается положительной; в противном случае э. д. с. входит в уравнение со знаком минус;
в) произвольные контуры выделяют так, чтобы каждый новый контур содержал хотя бы один участок цепи, не вошедший в те уже рассмотренные контуры, для которых уравнения, согласно второму правилу Кирхгофа, уже составлены.
Совокупность независимых уравнений, составленных по правилам Кирхгофа, оказывается достаточной, чтобы найти все токи, сопротивления или э. д. с. в разветвленной цепи. Задача сводится, таким образом, к решению системы линейных уравнений, в которой число уравнений должно совпадать с числом неизвестных величин.

Метод узловых потенциалов

Вторым методом, которым пользуются для решения сложных цепей, является метод узловых потенциалов. Этот метод основан на составлении уравнений по первому закону Кирхгофа:

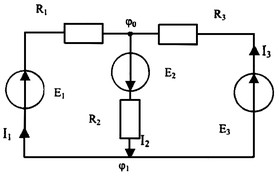
Схема сложной электрической цепи с двумя узлами.
Токи каждой из параллельных ветвей определяются как:

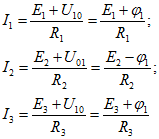
Напряжения между точками с заданными потенциалами при

Подставив полученные значения токов в первое уравнение

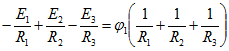
получим выражение для потенциала

При решении методом узловых потенциалов необходимо помнить, что в левой части уравнения знак ЭДС (+), если она направлена к рассматриваемому узлу, и знак (-), если от узла. В случае последовательного соединения сопротивлений в ветви

В общем виде уравнения узловых потенциалов имеют вид:

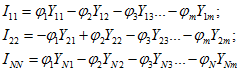
Если в схеме имеются источники тока, то слагаемое в правой части будет равно сумме источников тока:

Метод узловых потенциалов имеет преимущество, если число независимых узлов меньше числа контуров.
При наличии источников тока контура надо выбирать так, чтобы источники входили только в один контур. Тогда ток этого контура будет равен току источника.

Баланс мощности

На основании закона сохранения энергии мощность, развиваемая источниками электрической энергии, должна быть равна мощности преобразования в цепи электрической энергии в другие виды энергии: