Короткое замыкание rL-цепи
Ветвь с сопротивлением и индуктивностью, например реальная катушка, внезапно замыкается ключом накоротко (рис. 14.1). Ток в катушке до коммутации был постоянным
![]()
Найдем закон изменения тока в катушке.
Установившийся ток в катушке после коммутации равен нулю. Следовательно, ![]()
Свободный ток удовлетворяет однородному дифференциальному уравнению первого порядка
![]()
общее решение которого, как легко проверить подстановкой,
![]()
В (14.8) А — постоянная интегрирования и — r/L=р — корень характеристического уравнения![]()
соответствующего однородному дифференциальному уравнению (14.7).
При t=0 из (14.8) следует, что i(0)=i(0+) = А, и, так как по первому закону коммутации ![]() , т. е. при
, т. е. при ![]() имеем i(0+)=i(0-), то
имеем i(0+)=i(0-), то ![]()
Таким образом, после коммутации![]()
(рис. 14.2).
Рис. 14.1
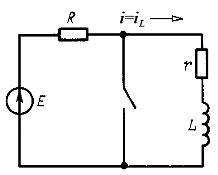
Рис. 14.2

Величина τ=L/r, имеющая размерность времени, называется постоянной времени rL-цепи и может быть определена как время, в течение которого свободный ток уменьшится в е раз по сравнению со своим начальным значением ![]() . В самом деле,
. В самом деле,
![]()
Для графического определения t проведем касательную к кривой ![]() в любой ее точке С. Значение подкасательной BD может быть найдено из треугольника CBD, а
в любой ее точке С. Значение подкасательной BD может быть найдено из треугольника CBD, а
![]()
где ![]() — масштабы, т. е. постоянная времени численно равна длине любой подкасательной. В частности, она численно равна длине подкасательной
— масштабы, т. е. постоянная времени численно равна длине любой подкасательной. В частности, она численно равна длине подкасательной ![]() для касательной
для касательной ![]() , проведенной в начальной точке
, проведенной в начальной точке ![]() .
.
Величина, обратная постоянной времени,
![]()
называется коэффициентом затухания rL-цепи. Свободный ток затухает тем медленнее, и, следовательно, новый принужденный режим не устанавливается тем дольше, чем больше постоянная времени τ или чем меньше коэффициент затухания α, т. е. чем больше индуктивность L и чем меньше сопротивление r.
Электродвижущая сила самоиндукции![]()
равна при t = 0 напряжению на сопротивлении r и в момент коммутации поддерживает значение тока на начальном уровне.
С энергетической точки зрения процесс короткого замыкания rL-цепи характеризуется тем, что вся энергия, запасенная до коммутации в магнитном поле катушки,![]()
в течение переходного процесса превращается в сопротивлении r в тепло: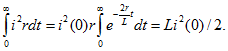
Заметим, что теоретически процесс исчезновения тока в короткозамкнутой катушке длится бесконечно долго, чем и объясняется необходимость в качестве верхнего предела у интеграла взять бесконечность. Однако практически для многих катушек этот переходный процесс закончится весьма быстро. Постоянная времени rL-цепи обычно лежит в пределах от нескольких микросекунд до долей секунды. Последнее значение относится к большим катушкам со стальным магнитопроводом и значительным числом витков.
Если до короткого замыкания в катушке был переменный ток, то характер переходного процесса нисколько не изменится, но i(0) равно значению тока в катушке i(0-) в момент короткого замыкания.
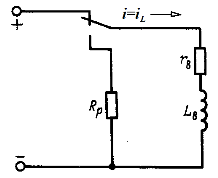
С переходным процессом в rL-цепи приходится считаться во многих случаях электротехнической практики, например при измерении сопротивления r обмотки трансформатора с большой индуктивностью (рис. 14.3), которая питается от источника постоянной ЭДС E через дополнительный резистор с сопротивлением R. Напряжение на обмотке измеряется милливольтметром. Если после отсчета показаний амперметра и милливольтметра отключить обмотку трансформатора от источника напряжения, то ее ток замкнется через милливольтметр. Так как ток обмотки трансформатора может быть достаточно большим и в момент отключения рубильника не изменяется скачком, то милливольтметр можно сжечь.
Обмотку возбуждения мощной электрической машины при необходимости быстро снять возбуждение не отключают от цепи питания (постоянное напряжение), а замыкают на разрядное сопротивление, в котором энергия магнитного поля превращается в тепло (рис. 14.4). Если просто разомкнуть цепь обмотки возбуждения, то даже при наличии электрической дуги ток очень быстро уменьшится до нуля (- di/dt будет очень велико). Так как обмотка возбуждения имеет большую индуктивность LB, то в ней возникает весьма значительная ЭДС самоиндукции ![]() , которая может пробить изоляцию на корпус машины или изоляцию между витками.
, которая может пробить изоляцию на корпус машины или изоляцию между витками.
Рис. 14.3
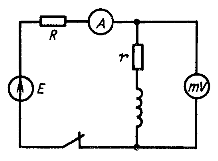
Рис. 14.4
Переходные процессы
Переходные процессы в электрических цепях
Законы коммутации
Переходный, установившийся и свободный процессы
Короткое замыкание rL-цепи
Включение rL-цепи на постоянное напряжение
Включение rL-цепи на синусоидальное напряжение
Короткое замыкание rС-цепи
Включение rC-цепи на постоянное напряжение
Включение rC-цепи на синусоидальное напряжение
Переходные процессы в rС-цепи
Апериодическая разрядка конденсатора
Предельный случай апериодической разрядки конденсатора
Периодическая (колебательная) разрядка конденсатора
Включение rLC-цепи на постоянное напряжение
Общий случай расчета переходных процессов классическим методом
Пример классического метода
Переходные процессы в цепях с взаимной индуктивностью
Включение пассивного двухполюсника к источнику непрерывно меняющегося напряжения
Включение пассивного двухполюсника к источнику напряжения произвольной формы
Переходная и импульсная переходная характеристики
Запись интеграла Дюамеля при помощи импульсной переходной характеристики
Метод переменных состояния
Численные методы решения уравнений состояния
Дискретные модели электрической цепи
Переходные процессы при некорректных коммутациях
Определение переходного процесса при воздействии периодических импульсов напряжения