В уравнениях (1.20), составленных по второму закону Кирхгофа, напряжение на любом сопротивлении можно всегда из 

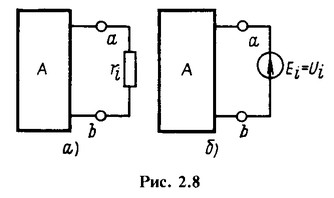
левой стороны перенести в правую со знаком минус и рассматривать как эквивалентную ЭДС , направленную противоположно току в ветви i. Это положение носит название принципа компенсации. Его иллюстрируют рис. 2.8, а и б, на которых прямоугольником с буквой А (активный) обозначены все участки цепи, кроме элемента с сопротивлением . Очевидно, что обе схемы эквивалентны, если , при этом следует иметь в виду, что эквивалентная ЭДС прямо пропорциональна току в ветви (закон Ома), т. е. зависит от тока. Таким образом, источник ЭДС, которым можно заменить любой резистивный элемент цепи, соответствует простейшему идеальному зависимому источнику, ЭДС которого зависит от тока по известному закону. Понятие о зависимом источнике широко применяется при анализе как линейных, так и нелинейных цепей. Сопротивление может быть и входным сопротивлением любого пассивного двухполюсника (см. раздел).
Любую ветвь с известным током можно заменить источником тока при этом режим цепи не изменится.