Для однозначного определения потенциала любой точки электрической цепи необходимо задать (произвольно) потенциал какой-нибудь одной точки. Выберем для схемы, представленной на рис. 1.7, а, . По определению потенциал точки 3 больше φ₂ на значение ЭДС:

Ток I во внешней части простейшей электрической цепи, а в общем случае в любом пассивном элементе цепи, а значит, и схемы, направлен, как указывалось, от точки с более высоким потенциалом (3) к точке с более низким (1). Поэтому потенциал φ₃ больше потенциала φ₁:

Из (1.9) и (1.10) имеем

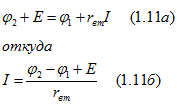
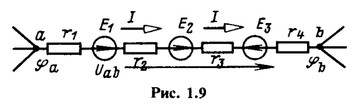
Аналогично можно написать формулу для тока участка сложной электрической схемы, состоящего из любого числа последовательно соединенных источников, представленных схемами замещения на рис. 1.7, и приемников при заданной разности потенциалов на концах этого участка (рис. 1.9). Ток I на участке схемы, содержащем источники ЭДС, может быть направлен от точки а к точке b или наоборот. Если направление тока заранее не известно, то для составления выражений, подобных (1.11), нужно выбрать направление тока произвольно. Такое произвольно выбранное направление тока условились называть положительным направлением и обозначать (как и выше действительное направление) стрелкой с просветом или отмечать индексами у буквы I.
Если принять за положительное направление тока I направление от точки а к точке b, то потенциал φ_b определяется через потенциал φ_a выражением

Из этого равенства следует

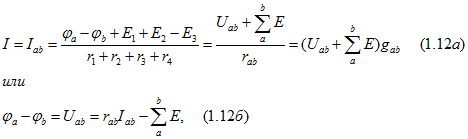
где — суммарное сопротивление участка схемы; — разность потенциалов или напряжение между выводами рассматриваемого участка, взятые по выбранному направлению тока;
— алгебраическая сумма ЭДС, действующих на том же участке, причем каждая ЭДС, направление действия которой совпадает с положительным направлением тока, записывается с положительным знаком, а в противном случае — с отрицательным.
Формула (1.12а) представляет собой закон Ома для участка цепи (схемы) с ЭДС (обобщенный закон Ома).
Если в результате расчета по (1.12а) для тока получается отрицательное значение, то это значит, что действительное направление тока не совпадает с выбранным положительным направлением (противоположно произвольно выбранному направлению).
Для напряжения между любыми точками цепи также может быть произвольно выбрано положительное направление. Положительное направление напряжения указывается индексами у буквы U или обозначается на схемах стрелкой, которую, например, для напряжения будем в дальнейшем ставить от точки а к точке b. Таким образом, напряжение, как и ток, при расчетах надо рассматривать как алгебраическую величину.
Для ЭДС источников напряжения и токов источников тока, если их действительные направления не известны, также выбираются произвольные положительные направления, которые указывают двойными индексами или обозначают стрелками.
На участках схемы с пассивными элементами положительные направления напряжения и тока будем всегда выбирать совпадающими. В этом случае отдельную стрелку для напряжения можно и не ставить.