Сложение синусоидальных функций времени
При исследовании цепей синусоидального тока приходится алгебраически суммировать. Гармонические функции времени одинаковой частоты, но с различными амплитудами и с различными начальными фазами. Непосредственное суммирование гармонических функций времени связано с трудоемкими и громоздкими тригонометрическими преобразованиями. Значительно проще эта задача решается графически при помощи векторной диаграммы или аналитически путем суммирования комплексных амплитуд.
Пусть требуется найти сумму двух гармонических функций времени![]()
 Сначала рассмотрим решение, выполняемое при помощи векторной диаграммы. Отложим векторы
Сначала рассмотрим решение, выполняемое при помощи векторной диаграммы. Отложим векторы ![]() и графически определим вектор
и графически определим вектор ![]() равный геометрической сумме векторов
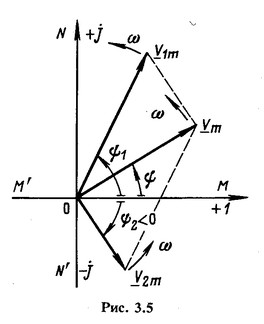
равный геометрической сумме векторов ![]() (рис. 3.5). Эта векторная диаграмма построена для случая, когда
(рис. 3.5). Эта векторная диаграмма построена для случая, когда ![]() .
.
Представим себе, что векторы ![]() с момента t=0 начинают вращаться вокруг начала координат О против направления движения часовой стрелки с постоянной угловой скоростью ω. Проекция вращающегося вектора
с момента t=0 начинают вращаться вокруг начала координат О против направления движения часовой стрелки с постоянной угловой скоростью ω. Проекция вращающегося вектора ![]() на вертикальную ось N’N в любой момент времени равна сумме проекций на эту же ось вращающихся векторов
на вертикальную ось N’N в любой момент времени равна сумме проекций на эту же ось вращающихся векторов ![]() , т. е. мгновенных величин
, т. е. мгновенных величин ![]() . Следовательно, проекция вектора
. Следовательно, проекция вектора ![]() на вертикальную ось равна искомой сумме
на вертикальную ось равна искомой сумме ![]() , а вектор
, а вектор ![]() изображает искомую синусоидальную функцию времени
изображает искомую синусоидальную функцию времени ![]() .
.
Таким образом, определив из диаграммы длину вектора ![]() и угол ψ, можем написать выражение искомой величины
и угол ψ, можем написать выражение искомой величины ![]() .
.
Теперь перейдем к аналитическому методу. Рассматривая векторы как комплексные амплитуды, на основании выполненного построения (рис. 3.5) можно написать![]()
Чтобы произвести суммирование комплексных чисел, их надо представить в алгебраической форме: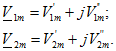
Выполнив суммирование, получим
![]()
где ![]()
Отсюда находим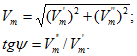
Так как ![]() , то для определения ψ нужно еще знать, в какой четверти располагается вектор
, то для определения ψ нужно еще знать, в какой четверти располагается вектор ![]() . Это легко устанавливается по знакам действительной и мнимой частей
. Это легко устанавливается по знакам действительной и мнимой частей ![]() . В расчетах начальную фазу ψ выражают или в радианах, или в градусах.
. В расчетах начальную фазу ψ выражают или в радианах, или в градусах.
Рассмотренные способы можно применить для сложения любого числа синусоидальных функций времени одинfковой частоты.
Обычно при расчетах цепей синусоидального тока необходимо знать только действующие величины для синусоидальных функций времени и их сдвиг по фазе относительно друг друга. В этих случаях при построении векторных диаграмм нужно точно соблюдать углы сдвига фаз между векторами, а положение осей координат можно выбрать произвольно или оси совсем не изображать. Кроме того, длины векторов часто берут равными не амплитудным, а действующим величинам.
Соответственно при аналитическом расчете начальные фазы можно изменить на один и тот же угол, например так, чтобы начальная фаза одной из рассматриваемых функций стала равной нулю. Вместо комплексных амплитуд часто берут значения, в ![]() раз меньшие, так называемые комплексные действующие величины:
раз меньшие, так называемые комплексные действующие величины:
![]()
Пример 3.3.
Даны токи ![]()
Определить ток ![]() , равный разности токов
, равный разности токов ![]() .
.
Решение.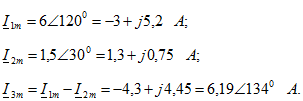
Следовательно, ![]()
Электрические цепи переменного тока
Расчет цепей переменного тока
Символический метод расчета цепей переменного тока
Переменные токи
Понятие о генераторах переменного тока
Синусоидальный ток
Действующие ток, ЭДС и напряжение
Изображение синусоидальных функций времени векторами и комплексными числами
Сложение синусоидальных функций времени
Электрическая цепь и ее схема
Последовательное соединение резистивного, индуктивного и емкостного элементов
Сопротивления
Разность фаз напряжения и тока
Напряжение и токи при параллельном соединении
Проводимости
Пассивный двухполюсник
Мощности
Мощности резистивного, индуктивного и емкостного элементов
Баланс мощностей
Знаки мощностей и направление передачи энергии
Определение параметров пассивного двухполюсника
Условия передачи максимальной мощности
Понятие о поверхностном эффекте и эффекте близости
Параметры и эквивалентные схемы конденсаторов
Параметры и эквивалентные схемы катушек индуктивности и резисторов