Трансформаторные подстанции высочайшего качества

Электрический ток неразрывно связан с магнитным и электрическим полями. При переменном токе эти поля изменяются во времени. Изменяющееся магнитное поле наводит ЭДС, изменение электрического поля сопровождается изменением зарядов на проводниках. В проводниках, в резисторах, а часто и в окружающей их среде электромагнитная энергия преобразуется в тепло. В различных машинах, аппаратах, приборах и других устройствах электромагнитная энергия преобразуется и в другие виды энергии (в механическую, химическую и т. д.); часть электромагнитной энергии излучается. В электрической цепи нельзя выделить какой-либо участок, с которым не были бы связаны эти явления.
Для того чтобы упростить исследование процессов в реальной электрической цепи переменного тока, ее, как и цепь постоянного тока, заменяют схемой замещения, или, короче, просто схемой (математической моделью), составленной из элементов, каждый из которых учитывает одно из этих явлений.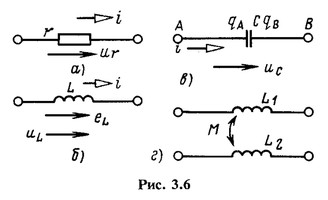
К пассивным элементам схемы при переменных токах относятся резистивный элемент с сопротивлением r, или, короче, сопротивление r, индуктивный элемент с индуктивностью L, или, короче, индуктивность L, и емкостный элемент с емкостью С, или, короче, емкость С. Их условные обозначения на схемах показаны на рис. 3.6, а -в.
Взаимная индуктивность между отдельными частями электрических устройств учитывается как взаимная индуктивность М между индуктивными элементами (рис. 3.6, г). Таким образом, взаимная индуктивность не является самостоятельным элементом схемы.

В резистивном элементе с сопротивлением r электромагнитная энергия преобразуется в тепло при мощности преобразования . Резистивные элементы вводят в схему также и для учета необратимого преобразования электромагнитной энергии в другие формы энергии (например, в механическую) и для учета излучаемой энергии.
Напряжение между выводами резистивного элемента и ток в элементе (рис. 3.6, а) связаны законом Ома:



Индуктивный элемент схемы с индуктивностью L (рис. 3.6, б) учитывает энергию магнитного поля и явление самоиндукции. При изменении тока в индуктивности возникает ЭДС самоиндукции . По закону Ленца она препятствует изменению тока. Поэтому при выборе положительных направлений для тока i и ЭДС одинаковыми (как на рис. 3.6, б и как это обычно принято делать) знаки и di/dt противоположны и . Для того чтобы через индуктивность проходил переменный ток, на ее выводах должно быть напряжение, равное и противоположное наведенной ЭДС. При одинаковых положительных направлениях напряжений и ЭДС они противоположны по знаку:

а при противоположном положительном направлении ЭДС

Емкостный элемент схемы с емкостью С (рис. 3.6, в) учитывает энергию электрического поля. На электродах емкости заряды равны и противоположны по знаку: , причем

Для указанных на рис. 3.6, в положительных направлений тока i и напряжения на емкости заряд и напряжение имеют одинаковые знаки, т. е. .
Ток в ветви с емкостью равен скорости изменения заряда на электродах, и при указанном положительном направлении тока знак тока совпадает со знаком производной по времени от заряда . Действительно, приросту заряда соответствует положительное значение тока, убыли заряда — отрицательное значение тока. Поэтому, обозначив , можно написать

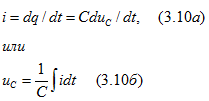
Схема зависит от частоты переменного тока. Так, при достаточно низкой частоте резистор может быть представлен сопротивлением, индуктивная катушка — последовательным соединением индуктивности и сопротивления, а конденсатор при хорошей изоляции между электродами — емкостью. С ростом частоты, как будет показано в следующих параграфах, увеличиваются ЭДС, обусловленные индуктивностями, и токи, обусловленные емкостями. Поэтому при высоких частотах приходится учитывать индуктивность проволочных резисторов и межвитковую емкость катушек. Кроме того, с увеличением частоты растут потери в изоляции конденсаторов. Для учета всех этих явлений приходится резисторы, индуктивные катушки и конденсаторы заменять более сложными схемами. При высоких частотах приходится также учитывать емкости между проводами, соединяющими различные элементы реальной электрической цепи, и вводить их в схему.
Если схема получается с ограниченным (конечным) числом элементов, то говорят, что реальная цепь рассматривается как цепь с сосредоточенными параметрами. Если же приходится пользоваться схемой, содержащей неограниченно большое (бесконечное) число элементов, говорят, что цепь рассматривается как цепь с распределенными параметрами.
Теперь рассмотрим вопрос о применимости к схемам цепей переменного тока законов Кирхгофа. На проводах и в узлах схемы не могут накапливаться заряды (единственными накопителями зарядов являются емкостные элементы). Поэтому для любого узла схемы справедлив первый закон Кирхгофа:
алгебраическая сумма мгновенных значений токов в проводах, соединенных в узел, равна нулю:

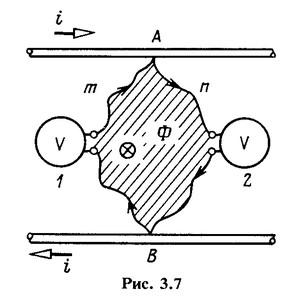Напряжение между двумя точками цепи переменного тока в общем случае зависит от пути, вдоль которого оно определяется. Выясним, например, каково различие в напряжениях между точками А и В двух проводов цепи переменного тока (рис. 3.7), определяемых по двум различным путям. Между точками А и В включены два вольтметра для измерения напряжения. Соединительные провода от первого вольтметра идут по пути АmВ, от второго вольтметра — по пути АnВ.
Согласно закону электромагнитной индукции напряжение вдоль замкнутого контура АnВmА равно ЭДС, индуктированной в этом контуре магнитным потоком Ф, пронизывающим поверхность, ограниченную контуром:



Заметим, что знак минус перед ставится в том случае, если положительное направление магнитного потока и положительное направление ЭДС (направление обхода контура) согласованы по правилу правого винта. В рассматриваемом случае положительное направление Ф выбрано от читателя за плоскость чертежа. Напряжение

Подставив это равенство в предыдущее выражение, получим

Следовательно, напряжения между двумя точками, определенные вдоль двух различных путей, отличаются друг от друга на ЭДС, индуктированную в замкнутом контуре, образованном этими двумя путями. При согласовании положительного направления ЭДС (направления обхода контура) и положи-тельного направления магнитного потока по правилу левого винта перед производной следует поставить не знак минус, а знак плюс.
Напряжения, определяемые вдоль различных путей, будут одинаковы только в том случае, если замкнутые контуры, образованные этими путями, не пронизываются переменным магнитным потоком.
В схеме замещения напряжения между различными ее точками от пути не зависят. Так, напряжения на выводах элементов схемы r, L и С связаны с током приведенными выше соотношениями (3.8) — (3.10) вне зависимости от путей (взятых вне элементов), по которым эти напряжения определяются. Поэтому точки схемы переменного тока можно, так же как и точки цепи постоянного тока, характеризовать потенциалами, а напряжения рассматривать как разности потенциалов. Имея это в виду, говорят, что схемы или идеализированные цепи потенциальны. Изменение потенциала по любому замкнутому контуру такой цепи равно нулю. Поэтому справедлива следующая формулировка второго закона Кирхгофа:
алгебраическая сумма мгновенных напряжений на всех элементах любого замкнутого контура схемы равна нулю:

или, иначе, алгебраическая сумма мгновенных ЭДС всех источников напряжения в любом замкнутом контуре схемы равна алгебраической сумме мгновенных напряжений на всех остальных элементах того же контура.
Выберем произвольный узел m из общего числа У. Ток в k-й ветви, соединяющей узел т с другими узлами, обозначим . По первому закону Кирхгофа (3.11а) для каждого m-го узла

Составим такие же равенства для всех У узлов и найдем их сумму:



В это тождество ток ветви входит 2 раза и с разными знаками (ток ветви направлен от одного из узлов к другому). Поэтому тождество, которое называется теоремой Телледжена можно записать и так:

где — напряжение или разность потенциалов между узлами той из В ветвей, ток в которой .
Произведение — это мгновенная мощность n-й ветви, и из тождества (3.12) следует баланс мощностей: суммарная мгновенная мощность всех ветвей равна нулю (закон сохранения энергии).
Так как теорема Телледжена получена из законов Кирхгофа, то она справедлива для каждого момента любого режима (установившегося и неустановившегося) и любых цепей. Можно показать, что тождество (3.12) остается справедливым при напряжении и токе , которые определяются для двух разных цепей (с разными параметрами), если у этих цепей одинаковы графы. Конечно, в последнем случае тождество (3.12) не соответствует балансу мощностей.
Здесь рассматриваются линейные цепи, содержащие источники энергии с синусоидальными ЭДС. Если в цепи действуют несколько источников энергии, то рассматриваются только те случаи, когда частоты ЭДС всех источников одинаковы. Заметим, что именно этот случай имеет место при нормальном режиме в электрических цепях энергетических систем.
Наконец, здесь рассматриваются так называемые установившиеся режимы цепей, которые наступают после некоторого промежутка времени (обычно от долей секунды до нескольких секунд) после окончания всех коммутаций (переключений) в цепи. При установившемся режиме токи и напряжения во всех ветвях и участках линейных цепей также синусоидальные и изменяются с той же частотой, что и ЭДС источников энергии.
Таким образом, в уравнения, выражающие законы Кирхгофа, входят алгебраические суммы синусоидальных функций времени, суммирование которых, как указывалось, целесообразно заменить суммированием изображающих их комплексных величин.
После такой замены получаются законы Кирхгофа для комплексных амплитуд или для комплексных действующих токов, напряжений и ЭДС:
алгебраическая сумма комплексных токов в проводниках, соединенных в узел, равна нулю. Алгебраическая сумма комплексных напряжений на всех элементах любого замкнутого контура схемы равна нулю, или, иначе, алгебраическая сумма комплексных ЭДС всех источников напряжения в любом замкнутом контуре схемы равна алгебраической сумме комплексных напряжений на всех остальных элементах того же контура.