Мощность в цепи несинусоидального тока

Активная мощность периодического тока произвольной формы определяется как средняя мощность за период

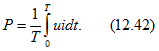
Если мгновенные значения напряжения и тока выразить в виде тригонометрических рядов, то получим

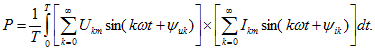
Так как среднее за период значение произведения мгновенных значений синусоид различной частоты равно нулю (см. раздел) и тригонометрические ряды абсолютно сходятся при любых частотах w, то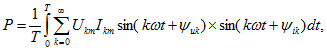

или после интегрирования

где .

Из этого выражения следует очень важный вывод, что средняя мощность несинусоидального тока равна сумме средних мощностей отдельных гармоник (постоянная составляющая рассматривается как нулевая гармоника с ):

(равенство Парсеваля).
Полученная таким образом мощность представляет собой активную мощность или энергию, необратимо преобразуемую в единицу времени в данном участке цепи в тепловую, механическую или какую-либо иную форму энергии.
Кроме понятия активной мощности Р по аналогии с синусоидальными токами вводится понятие полной мощности S, определяемой как произведение действующих значений тока и напряжения:

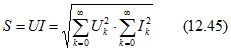
Активная мощность меньше полной; исключение составляет только мощность в цепи, сопротивление которой — чисто активное, т. е. , и, следовательно, S = Р.
Отношение активной мощности к полной называют коэффициентом мощности и иногда приравнивают косинусу некоторого условного угла ϑ:

Можно дать геометрическую интерпретацию углу ϑ, пользуясь понятием эквивалентных синусоид тока и напряжения, действующие значения которых равны действующим значениям несинусоидальных величин. Если между эквивалентными синусоидами напряжения и тока будет такой угол сдвига фаз, при котором мощность, выделяемая в цепи, равняется мощности несинусоидального тока, то этот угол сдвига и равен условному углу ϑ.
Формально можно ввести понятие реактивной мощности, определяемой как сумма реактивных мощностей отдельных гармоник:

Для несинусоидальных токов в отличие от синусоидальных квадрат полной мощности обычно больше суммы квадратов активной и реактивной мощностей:

В цепях передачи сигналов (несинусоидальные функции) отсутствуют искажения, если сопротивление приемника (см. рис. 3.22) равно внутреннему сопротивлению источника , так как в этом случае при любой частоте напряжение приемника равно половине ЭДС источника.

Пример 12.11. Вычислить Р, Q и S, если напряжение и ток состоят из двух гармоник: 1-й и 3-й. Известны действующие значения гармоник напряжения и тока , а также углы сдвига фаз между гармониками напряжения и тока .
Решение. В этом случае мощности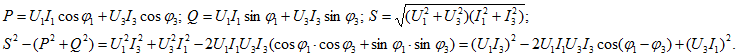

Очевидно, что только при условиях и . Оба эти условия выполняются только при чисто активном сопротивлении приемника, т. е. при одинаковых формах кривых тока и напряжения.

Несинусоидальные токи и напряжения