Трансформаторные подстанции высочайшего качества

В предшествующих главах рассматривались линейные цепи с неизменными параметрами r, L, С и M при действии источников постоянных или синусоидальных ЭДС или токов.
На практике ЭДС, напряжения и токи обычно в большей или меньшей степени отличаются от постоянных или синусоидальных, причем зависимость от времени может быть периодической, почти периодической и непериодической.
В машинных генераторах переменного тока вследствие отличия кривой распределения магнитной индукции вдоль зазора от синусоиды кривые наводимых в обмотках ЭДС отличаются от синусоидальных. В цепях, содержащих элементы с нелинейными сопротивлениями, индуктивностями или емкостями (например, вентиль, электрическую дугу, катушку со стальным магнитопроводом), даже при синусоидальных ЭДС возникают несинусоидальные токи и несинусоидальные напряжения. Так, на рис. 12.1 показаны примеры кривых тока в цепи с насыщающимся реактором (рис. 12.1, а) и в цепи управляемого вентиля (рис. 12.1,6).
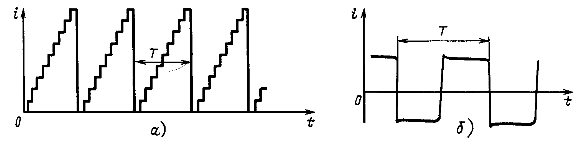
Генераторы периодических импульсов применяются в различных устройствах радиотехники, автоматики, телемеханики, вычислительной техники, обработки данных, в автоматизированных системах управления. Форма импульсов может быть различной: пилообразной (рис. 12.2, а и б), ступенчатой (рис. 12.3, а) и прямоугольной (рис. 12.3, 6). При прохождении этих импульсов через различные электрические цепи их форма существенно изменяется.
На рис. 12.1 — 12.3 все кривые строго периодичны (период повторения Т) и представляют собой примеры несинусоидальных периодических токов.
При передаче, например, радиотелеграфных и телефонных сигналов встречаются кривые тока, которые не строго периодичны, но имеют периодически изменяющуюся огибающую с периодом и на малом интервале времени могут считаться синусоидальными с периодом . При несоизмеримости и нет такого периода Т, через который эти кривые в точности повторяются. Поэтому их нельзя назвать периодическими, но они очень близки по своим свойствам к периодическим кривым и могут быть названы почти периодическими (в частном случае, когда , где k — целое число, эти кривые периодические с периодом ). Примером почти периодической кривой является ток в цепи динамика радиоприемника при передаче периодически изменяющегося звука.
Кроме указанных типов несинусоидальных кривых с явно выраженным периодом повторения мгновенных значений или огибающей часто приходится иметь дело с непериодическими кривыми, т. е. с кривыми, у которых нет периода повторения. Эти кривые могут быть вполне определенными, как, например, при передаче последовательности импульсов, но могут быть и случайными, например, в случае шумов и помех.

Во всех задачах, где приходится иметь дело со сложными несинусоидальными кривыми токов и напряжений, очень важно уметь свести сложную задачу к более простой и применить методы расчета более простых задач. В настоящей главе рассматриваются методы расчета линейных цепей при несинусоидальных периодических или почти периодических токах и напряжениях, которые можно разложить на гармонические составляющие.

Рис. 12.1

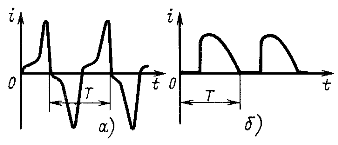
Рис. 12.2

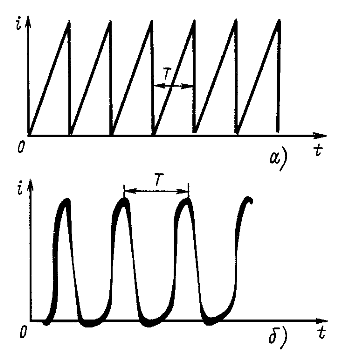
Рис. 12.3