Изображение синусоидальных функций времени векторами и комплексными числами

Расчет цепей переменного тока облегчается, если изображать синусоидально изменяющиеся токи, напряжения, ЭДС и т. д. векторами или комплексными числами.
Предположим, что некоторая величина (ток, напряжение, магнитный поток и т. п.) изменяется по синусоидальному закону:

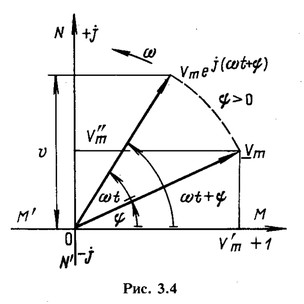Возьмем прямоугольную систему осей MON (рис. 3.4). Расположим под углом ψ относительно горизонтальной оси ОМ вектор , длина которого в выбранном масштабе равна амплитуде (положительные углы ψ откладываются против, а отрицательные — по направлению движения часовой стрелки). Представим себе, что вектор с момента t=0 начинает вращаться вокруг начала координат О против направления движения часовой стрелки с постоянной угловой скоростью, равной угловой частоте ω. В момент времени t вектор составит с осью ОМ угол . Его проекция на ось N’N равна в выбранном масштабе мгновенному значению рассматриваемой величины υ.
Мгновенные значения и как проекции вектора на ось N’N можно получить и другим путем, оставляя вектор неподвижным и вращая, начиная с момента t=0, ось N’N по направлению движения часовой стрелки с угловой скоростью ω. В этом случае вращающуюся ось N’N называют линией времени.

Таким образом, между мгновенным значением υ и вектором можно установить однозначную связь. На этом основании вектор называют вектором, изображающим синусоидальную функцию времени, или, кратко, вектором величины υ. Так, например, говорят о векторах напряжения, ЭДС, тока, магнитного потока и т. д. Конечно, эти векторы имеют смысл, отличный от смысла векторов, определяющих физические величины в пространстве, к которым относятся векторы скорости, силы, ускорения, напряженности электрического поля и т. п.
Векторы, изображающие синусоидальные функции времени, будем обозначать подчеркнутыми прописными (большими) буквами. Совокупность векторов, изображающих рассматриваемые синусоидальные функции времени, называется векторной диаграммой.
Если считать оси ММ’ и NN’ осями действительных и мнимых величин на комплексной плоскости, то вектор соответствует комплексному числу, модуль которого равен и аргумент — углу ψ. Это комплексное число называется комплексной амплитудой рассматриваемой величины.
Комплексную амплитуду можно записать в полярной, показательной, тригонометрической и алгебраической формах:

где
Если вектор , начиная с момента времени t=0, вращается против направления движения часовой стрелки с угловой скоростью w, то ему соответствует комплексная функция времени, которая называется комплексной мгновенной величиной:

Значение ее мнимой части равно рассматриваемой синусоидально изменяющейся величине υ.
Таким образом, величина с и ее изображение — комплексная амплитуда — однозначно связаны следующим равенством:

где символ Im обозначает, что от комплексной функции времени, записанной в квадратных скобках, берется только значение мнимой части.
Если гармонически изменяющуюся величину представить в виде косинусоидальной функции времени, то ее мгновенное значение

где символ Re обозначает действительную часть комплексной функции времени, записанной в скобках. В этом случае мгновенное значение u определяется графически как проекция вращающегося вектора на ось действительных величин.
Метод расчета цепей синусоидального тока, основанный на изображении гармонических функций времени комплексными числами, называется методом комплексных величин, методом комплексных амплитуд или комплексным методом расчета.
Комплексный метод был введен в электротехнику американским ученым и инженером Ч. П. Штейнметцем.

Пример 3.1.
Написать комплексную амплитуду тока

Решение.
Комплексная амплитуда .
Заданный ток равен мнимой части комплексной функции времени

Пример 3.2.
Комплексная амплитуда напряжения , частота f=1 кГц. Написать выражение для мгновенного напряжения.

Решение.
Угловая частота рад/с, амплитуда , так как действительная часть комплексной амплитуды отрицательная, а мнимая часть положительная, то вектор находится во второй четверти и, следовательно, .
Таким образом, мгновенное значение напряжения