Трансформаторные подстанции высочайшего качества

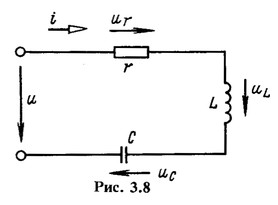
Пусть в ветви (рис. 3.8), состоящей из последовательно соединенных элементов r, L и С, т. е. в последовательном контуре или rLC-цепи, известен ток

Выясним, каковы напряжения на отдельных элементах и на входе.
На основании второго закона Кирхгофа

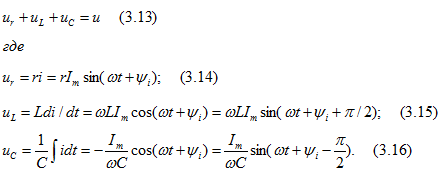
Постоянная интегрирования в выражении для принята равной нулю, так как в установившемся режиме, как уже указывалось, напряжение на любом участке цепи синусоидальное.
Из полученных выражений для видно, что напряжение на сопротивлении совпадает по фазе с током, напряжение на индуктивности опережает ток по фазе на угол π/2, а напряжение на емкости отстает по фазе от тока на угол π/2.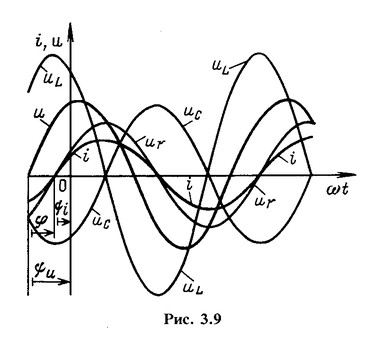

На рис. 3.9 показаны кривые мгновенных значений тока и напряжений в случае, если амплитуда напряжения на индуктивности больше амплитуды напряжения на емкости . Синусоида совпадает по фазе с синусоидой тока, а синусоиды сдвинуты относительно синусоиды тока на угол π/2 соответственно влево (опережение) и вправо (отставание). Таким образом, напряжения на индуктивности и на емкости сдвинуты относительно друг друга по фазе на угол π (находятся в противофазе).
Ординаты кривой напряжения

согласно (3.13) равны алгебраической сумме ординат кривых .
Определение напряжения н сводится к вычислению амплитуды Um и начальной фазы , которые могут быть найдены непосредственным суммированием трех синусоидальных функций времени с последующими тригонометрическими преобразованиями. Однако, как указывалось, проще всего задача решается комплексным методом.
Запишем комплексный ток и комплексные напряжения на основании выражений для их мгновенных значений:

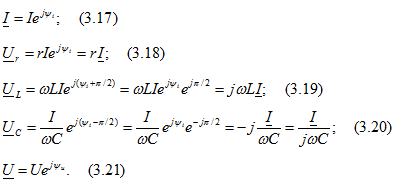
В выражениях для учтено, что

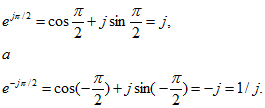
Сопоставив выражения для мгновенных напряжений (3.15), (3.16) с комплексными напряжениями (3.19), (3.20), можно установить простое правило перехода от производной и интеграла синусоидальной функции времени к изображающим их комплексным величинам: синусоидальная функция заменяется изображающей ее комплексной величиной, дифференцирование заменяется умножением на jw, а интегрирование — делением на jw.
Сумме синусоидальных напряжений (3.13) соответствует сумма изображающих их векторов или комплексных действующих напряжений:

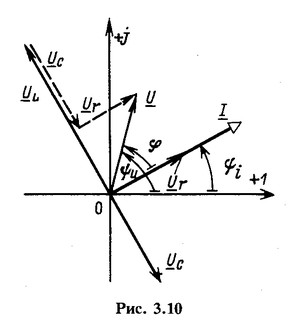
Это соотношение представляет собой уравнение по второму закону Кирхгофа, записанное в комплексной или векторной форме; оно представлено на векторной диаграмме (рис. 3.10). Напряжение совпадает по фазе с током i, поэтому вектор направлен одинаково с вектором I. Напряжение опережает по фазе i на π/2, поэтому вектор сдвинут относительно вектора I на угол π/2 «вперед» (против направления движения часовой стрелки). Напряжение отстает по фазе от i на π/2, поэтому вектор сдвинут относительно вектора I на угол π/2 «назад» (по направлению движения часовой стрелки).
Соображения о взаимном расположении векторов напряжения и тока непосредственно следует и из записи выражений комплексных напряжений .
Вектор (3.18) получается умножением I на действительную величину r. Аргумент комплексной величины rI такой же, как и комплексного тока I, поэтому направление вектора совпадает с направлением вектора I. Вектор (3.19) получается умножением I на . Умножение тока I на действительную величину не изменяет аргумента, а умножение на увеличивает аргумент на π/2. Следовательно, вектор повернут относительно вектора I на угол π/2 «вперед». Вектор (3.20) получается делением I на . Деление комплексной величины на не изменяет аргумента, а деление на j, равносильно умножению на уменьшает аргумент на π/2. Следовательно, вектор повернут относительно вектора I на угол π/2 «назад».
Так как умножение и деление вектора на j приводят к повороту вектора на π/2 соответственно «вперед» и «назад», то множитель j часто называют оператором поворота на π/2.
Сложив векторы , получим вектор U. Его длина определяет действующее напряжение , а положение относительно координатных осей — начальную фазу .
Решим ту же задачу аналитически. Теперь уравнение (3.22) будем рассматривать как соотношение между комплексными числами. Подставив в него значения комплексных напряжений, получим

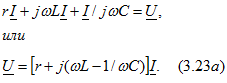
Это соотношение между комплексным напряжением и током называют законом Ома в комплексной форме. Записав комплексные величины в показательной форме, получим

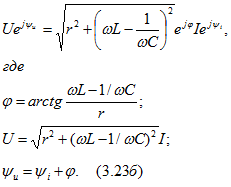
Так как то


Таким образом, амплитуда и начальная фаза напряжения на выводах контура определены и можно записать выражение для мгновенного напряжения:

В заключение отметим, что уравнение для комплексных токов и напряжений и векторные диаграммы взаимно связаны. Уравнения можно рассматривать как запись геометрических суммирований векторов, выполняемых на векторной диаграмме, и, наоборот, векторную диаграмму можно рассматривать как графическое представление соотношений между комплексными величинами в уравнении.