Трансформаторные подстанции высочайшего качества

Если в разветвленной цепи сопротивление одной из ветвей, например сопротивление второй ветви, изменяется, а все остальные сопротивления и ЭДС (токи) источников энергии неизменны, то, как было показано в разделе, токи и напряжения любых ветвей связаны линейными зависимостями. Это справедливо и для цепей синусоидального тока. В частности, для тока в первой ветви и тока во второй справедливо соотношение

где — комплексные числа.
На рис. 9.8 показана разветвленная цепь, в которой выделены источник напряжения в первой ветви и одно из сопротивлений , входящее в состав второй ветви. Остальная часть цепи, которая может содержать источники питания (активная цепь), показана в виде активного четырехполюсника А.
Пусть (модуль сопротивления ) изменяется, а аргумент остается неизменным; тогда, рассматривая всю цепь относительно сопротивления как активный двухполюсник, придем к заключению, что конец вектора перемещается по дуге окружности. Покажем, что в этом случае диаграммой тока также является дуга окружности.

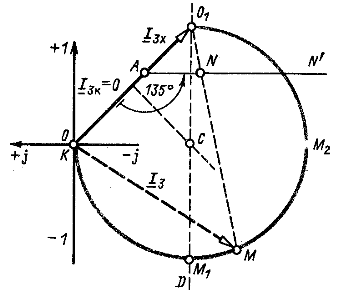
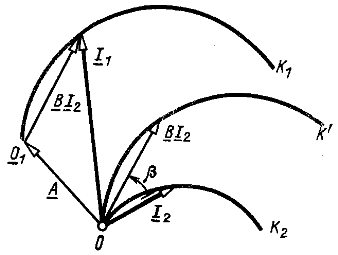
Пусть дуга (рис. 9.9) представляет круговую диаграмму тока . Умножение на приводит к изменению длины вектора в b раз и к повороту его на угол . Поэтому диаграмма вектора представляется дугой окружности ОК’, проходящей через точку О, повернутой относительно дуги на угол и имеющей радиус, в b раз больший радиуса дуги . Перенеся дугу ОК’ параллельно вектору на отрезок, равный длине вектора , получим дугу Конец вектора как это следует из построения, находится на дуге окружности т. е. дуга — круговая диаграмма тока Итак, если в какой-либо ветви разветвленной цепи изменяется только модуль одного из сопротивлений и остаются неизменными ЭДС (токи) всех источников питания, то годографом вектора тока любой из ветвей служит круговая диаграмма. Так как напряжения и токи любых ветвей связаны линейными зависимостями, то и для всех изменяющихся напряжений получаются годографы — круговые диаграммы.
Чтобы определить комплексы линейного соотношения (9.6), нужно знать токи для каких-либо двух режимов при двух различных значениях , например при
При (т. е. при разомкнутой ветви 2) и ток . Согласно (9.6) , откуда , т.е. коэффициент равен току в ветви 1 при разомкнутой ветви 2. При (т. е. при коротком замыкании ветви 2) обозначим токи Подставив эти значения в (9.6), получим

откуда

и, следовательно,

Рис. 9.8

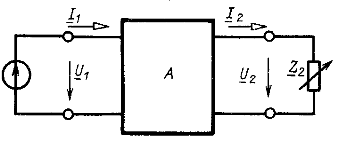
Рис. 9.9

Обозначим через напряжение на разомкнутых выводах ветви 2 и через входное сопротивление всей остальной цепи, рассматриваемой как активный двухполюсник относительно выводов ветви 2. По принципу эквивалентного генератора

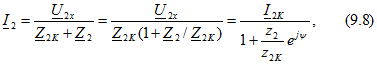
где
Подставив (9.8) в (9.7), получим

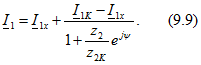
Второе слагаемое имеет такой же вид, как и (9.3), и, следовательно, графически может быть представлено круговой диаграммой с хордой
Для построения круговой диаграммы тока нужно предварительно определить

Построение круговой диаграммы выполняем в следующем порядке:
1) выбираем масштаб и откладываем вектор (рис. 9.10);
2) выбираем масштаб и откладываем векторы (отрезок ) и (отрезок ОК). Построение круговой диаграммы приводится для случая ;
3) соединяем точки , получаем хорду ;
4) выбираем масштаб и откладываем на хорде отрезок ;
5) проводим прямую изменяющегося параметра AN’ под углом к хорде , рассматриваемой как отрезок, имеющий направление от точки к точке К (построение круговой диаграммы приведено для случая , и поэтому на рис. 9.10 этот угол отложен относительно против направления движения часовой стрелки);
6) проводим прямую ;
7) на пересечении перпендикуляра к середине хорды с линией находим центр С круговой диаграммы.
Для любого значения можно отложить отрезок и на пересечении линии с круговой диаграммой в точке М найти положение конца вектора тока .

Рис. 9.10

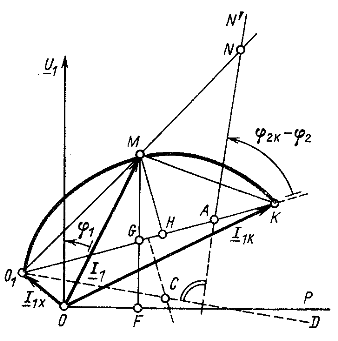
Из сказанного выше следует, что дуга , рассматриваемая относительно точки , представляет пропорционально измененную и повернутую на некоторый угол круговую диаграмму активного двухполюсника. Под активным двухполюсником здесь подразумевается вся цепь, представленная на рис. 9.8, за исключением сопротивления . Поэтому ток , напряжение , мощности определяются теми же отрезками прямых, которые служили для этой цели в круговой диаграмме двухполюсника. Ток определяется отрезком , напряжение — отрезком МК, а мощности — отрезком МН, или, что удобнее, пропорциональным ему отрезком MG.
Для определения масштабов нужно вычислить значения этих величин для каких-либо частных режимов и затем разделить эти значения на длины соответствующих им отрезков диаграммы. Например, вычислим . На диаграмме току и напряжению соответствует хорда . Следовательно, масштаб и масштаб

Пример 9.2. В цепи, показанной на рис. 9.11, изменяется от 0 до . Построить круговую диаграмму тока и определить по ней значения в двух режимах при и при
Решение. Находим величины, необходимые для построения круговой диаграммы и для определения масштабов:

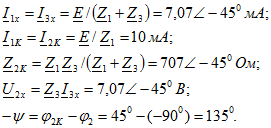
Выбираем масштаб и откладываем векторы (рис. 9.12). Обратим внимание, что на рис. 9.12 система координатных осей повернута на 90° против движения часовой стрелки по сравнению с ее обычным расположением. Ось положительных действительных величин направлена вверх, а ось положительных мнимых — влево. Такое расположение осей применяют часто, желая направить вектор напряжения или ЭДС вертикально при нулевой начальной фазе. Заметим, что такое расположение вектора напряжения было и на рис. 9.4 и 9.10. На рис. 9.12 вектор ЭДС не изображен, поскольку он не нужен для решения задачи.
Проводим хорду . Выбираем масштаб и откладываем отрезок Из точки А под углом проводим линию изменяющегося параметра AN’. Опускаем перпендикуляр на линию AN’ и восстанавливаем перпендикуляр к середине хорды . Получаем точку С — центр круговой диаграммы.
Ток измеряется отрезком ОМ, ток — отрезком , напряжение — отрезком КМ, сопротивление — отрезком AN. Масштабы были выбраны, масштабы
Ток если отрезок имеет наибольшую длину, т. е. если точка М занимает положение .

Рис. 9.11

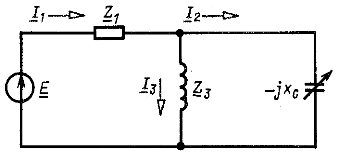
Рис. 9.12

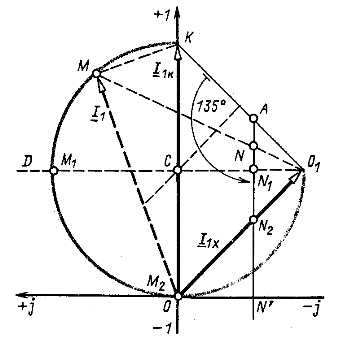
Ток если отрезок имеет наибольшую длину, т. е. если точка М занимает положение . Напряжение если отрезок КМ имеет наибольшую длину, т. е. если точка М занимает положение , совпадающее с точкой О. Значения переменных величин, соответствующих точке , обозначим одним штрихом, а точке — двумя штрихами. Найдем

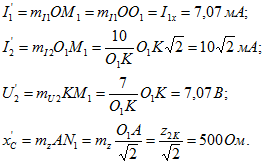
В проведенном подсчете учтены следующие соотношения между длинами отрезков, очевидные из рассмотрения диаграммы:

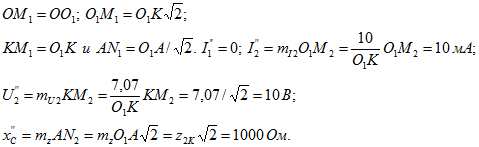
Точка соответствует резонансу токов. Так как рассматривается теоретический случай отсутствия потерь в ветвях 2 и 3, то

Пример 9.3. Для той же цепи (см. рис. 9.11) построить при изменении круговую диаграмму для тока и отметить на ней точки , соответствующие Найти для этих режимов значения тока
Решение. При имеем . Все остальные параметры, необходимые для построения круговой диаграммы тока , вычислены в предыдущем примере.
Выбрав масштаб , откладываем вектор (рис. 9.13). Так как , то конец вектора — точка К — совпадает с точкой О. Выбрав масштаб , откладываем отрезок Из точки А под углом проводим линию переменного параметра AN’. Затем определяем центр С окружности и строим круговую диаграмму. Отрезками измеряются соответственно Масштабы были выбраны, масштабы Ток в точке . Напряжение в точке . Из диаграммы находим

Рис. 9.13