Круговые диаграммы неразветвленной цепи и активного двухполюсника
Рассмотрим схему неразветвленной цепи (рис. 9.3), состоящую из последовательно соединенных элемента с неизменным сопротивлением ![]() и приемника с сопротивлением
и приемника с сопротивлением ![]() , аргумент которого неизменен, а модуль
, аргумент которого неизменен, а модуль ![]() изменяется в пределах от 0 до
изменяется в пределах от 0 до ![]() . Положим для определенности, что
. Положим для определенности, что ![]() . Найдем геометрическое место конца вектора тока при заданном неизменном напряжении
. Найдем геометрическое место конца вектора тока при заданном неизменном напряжении ![]() .
.
Ток
![]()
ничем не отличается от выражения (9.3), в котором ![]() соответствует
соответствует ![]() соответствует
соответствует ![]() .
.
Следовательно, конец вектора ![]() перемещается по дуге окружности.
перемещается по дуге окружности.
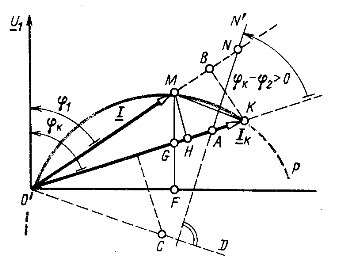
Построение круговой диаграммы может быть выполнено в следующем порядке:
1. Выбираем масштаб ![]() для напряжения
для напряжения ![]() и откладываем вектор
и откладываем вектор ![]() (рис. 9.4).
(рис. 9.4).
2. Вычисляем ток при ![]() , т. е. при коротком замыкании на выводах приемника (n = 0).
, т. е. при коротком замыкании на выводах приемника (n = 0).
3. Выбираем масштаб для тока ![]() и откладываем вектор
и откладываем вектор ![]() . Он представится отрезком
. Он представится отрезком ![]() , повернутым относительно
, повернутым относительно ![]() на угол
на угол ![]() . Отрезок ОК является хордой круговой диаграммы.
. Отрезок ОК является хордой круговой диаграммы.
4. Выбираем масштаб сопротивлений ![]() и вдоль прямой ОК откладываем отрезок
и вдоль прямой ОК откладываем отрезок ![]()
5. Из точки А под углом ![]() к вектору
к вектору ![]() проводим линию изменяющегося параметра AN’.
проводим линию изменяющегося параметра AN’.
6. Из начала координат проводим прямую ![]() .
.
7. Находим центр С круговой диаграммы как точку пересечения прямой OD и перпендикуляра, восстановленного из середины хорды ОК.
8. Проводим дугу круговой диаграммы. Эта дуга ограничена хордой ОК и лежит с той же стороны относительно хорды, где расположена линия AN’.
Ток ![]() для любого значения
для любого значения ![]() находим из диаграммы простым построением. Откладываем отрезок
находим из диаграммы простым построением. Откладываем отрезок ![]() , и точку N соединяем прямой с точкой О. Отрезок ОМ этой прямой от точки 0 до пересечения с окружностью и представляет вектор тока
, и точку N соединяем прямой с точкой О. Отрезок ОМ этой прямой от точки 0 до пересечения с окружностью и представляет вектор тока ![]() . При изменении
. При изменении ![]() от 0 до
от 0 до ![]() точка М (конец вектора
точка М (конец вектора ![]() ) перемещается от точки К до точки О.
) перемещается от точки К до точки О.
Покажем, как из круговой диаграммы можно получить различные величины, характеризующие режим цепи.
При заданном напряжении ![]() на выводах цепи ток пропорционален полной проводимости цепи
на выводах цепи ток пропорционален полной проводимости цепи ![]() , поэтому отрезок ОМ может служить мерой полной проводимости цепи. Масштаб для проводимости определим по режиму короткого замыкания, при котором проводимость измеряется отрезком ОК:
, поэтому отрезок ОМ может служить мерой полной проводимости цепи. Масштаб для проводимости определим по режиму короткого замыкания, при котором проводимость измеряется отрезком ОК: ![]() В этом же масштабе можно
В этом же масштабе можно
определить активную и реактивную проводимости цепи как проекции отрезка ОМ на ось, совпадающую с вектором ![]() и ось ОР, ей перпендикулярную.
и ось ОР, ей перпендикулярную.
Рис. 9.3
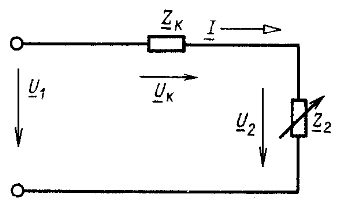
Рис. 9.4
Если ![]() , т.е.
, т.е. ![]() считается действительным числом (на рис. 9.4 ось действительных величин направлена вверх), то
считается действительным числом (на рис. 9.4 ось действительных величин направлена вверх), то ![]() имеют одинаковые аргументы и круговая диаграмма для тока в масштабе
имеют одинаковые аргументы и круговая диаграмма для тока в масштабе ![]() является круговой диаграммой комплексной проводимости цепи.
является круговой диаграммой комплексной проводимости цепи.
Из диаграммы имеем
![]()
где ![]()
Длины отрезков ОК, ОМ и МК пропорциональны напряжениям ![]() Напряжения
Напряжения ![]() можно определять по отрезкам ОМ и МК, пользуясь масштабом
можно определять по отрезкам ОМ и МК, пользуясь масштабом ![]()
Направления векторов ![]() (на диаграмме не показаны) отличаются от направлений векторов
(на диаграмме не показаны) отличаются от направлений векторов ![]() на угол
на угол ![]()
Длина перпендикуляра MF, опущенного из точки М на линию ОР, определяет активную мощность ![]() на входе цепи. Действительно,
на входе цепи. Действительно,
![]()
где ![]() — масштаб мощности
— масштаб мощности ![]()
Отрезок OF прямой ОР пропорционален реактивной мощности ![]() на входе цепи. Действительно,
на входе цепи. Действительно,
![]()
Покажем еще, что полную ![]() , активную
, активную ![]() и реактивную
и реактивную ![]() мощности можно определить отрезком MG перпендикуляра MF к линии ОР или длиной перпендикуляра МН, опущенного из точки М на хорду ОК. Опустим из точки К перпендикуляр КВ на прямую ON. Площадь треугольника ОМК равна:
мощности можно определить отрезком MG перпендикуляра MF к линии ОР или длиной перпендикуляра МН, опущенного из точки М на хорду ОК. Опустим из точки К перпендикуляр КВ на прямую ON. Площадь треугольника ОМК равна:
![]()
Угол ![]() не зависит от положения точки М. В полученном выражении для площади треугольника ОМК все сомножители, кроме
не зависит от положения точки М. В полученном выражении для площади треугольника ОМК все сомножители, кроме ![]() , постоянны. Следовательно, площадь треугольника пропорциональна
, постоянны. Следовательно, площадь треугольника пропорциональна ![]() . Так как
. Так как ![]() , то площадь треугольника пропорциональна также
, то площадь треугольника пропорциональна также ![]() У треугольника ОМК сторона ОК постоянна, поэтому его площадь пропорциональна высоте МН (ОК принята за основание треугольника) или отрезку MG, который пропорционален МН.
У треугольника ОМК сторона ОК постоянна, поэтому его площадь пропорциональна высоте МН (ОК принята за основание треугольника) или отрезку MG, который пропорционален МН.
Масштабы ![]() можно определить, вычислив мощности
можно определить, вычислив мощности ![]() для любого частного режима и разделив полученные значения на длину отрезка MG.
для любого частного режима и разделив полученные значения на длину отрезка MG.
Например, исходя из режима, отмеченного на диаграмме точкой М, имеем
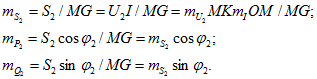
Пользуясь круговой диаграммой, можно определить зависимости ![]()
Для этого, задавшись значением ![]() , отложим соответствующий отрезок AN и определим положения точки М — конца вектора
, отложим соответствующий отрезок AN и определим положения точки М — конца вектора ![]() . Затем проведем отрезки МК, MF и MG и замерим их длины; наконец, пользуясь масштабами, вычислим соответствующие этим отрезкам величины. Вообще же по круговой диаграмме можно найти зависимость всех перечисленных выше величин от любой из них, принятой за независимую переменную. Вычерчивая ряд отрезков, изображающих величину, которая принята за независимую переменную, нетрудно построить отрезки, определяющие остальные величины.
. Затем проведем отрезки МК, MF и MG и замерим их длины; наконец, пользуясь масштабами, вычислим соответствующие этим отрезкам величины. Вообще же по круговой диаграмме можно найти зависимость всех перечисленных выше величин от любой из них, принятой за независимую переменную. Вычерчивая ряд отрезков, изображающих величину, которая принята за независимую переменную, нетрудно построить отрезки, определяющие остальные величины.
Рассмотренная круговая диаграмма для неразветвленной цепи применима к любому активному двухполюснику, сопротивление нагрузки которого изменяется так, что угол ![]() Это утверждение следует из принципа эквивалентного генератора, согласно которому активный двухполюсник с сопротивлением нагрузки
Это утверждение следует из принципа эквивалентного генератора, согласно которому активный двухполюсник с сопротивлением нагрузки ![]() можно представить схемой по рис. 9.3, в которой
можно представить схемой по рис. 9.3, в которой ![]() — входное сопротивление активного двухполюсника, a
— входное сопротивление активного двухполюсника, a ![]() — напряжение на выводах двухполюсника при холостом ходе.
— напряжение на выводах двухполюсника при холостом ходе.
Пример 9.1. Построить круговую диаграмму для тока ![]() в неразветвленной части цепи рис. 9.5 при изменении емкости С, считая, что остальные параметры цепи
в неразветвленной части цепи рис. 9.5 при изменении емкости С, считая, что остальные параметры цепи ![]() , а также частота и напряжение питания неизменны.
, а также частота и напряжение питания неизменны.
Решение. Ток ![]() Ток
Ток ![]() неизменный, а ток
неизменный, а ток ![]() изменяется по круговой диаграмме. Заметим, что
изменяется по круговой диаграмме. Заметим, что ![]() в схеме рис. 9.5 соответствуют сопротивлениям
в схеме рис. 9.5 соответствуют сопротивлениям ![]() в схеме рис. 9.3 и комплексным величинам
в схеме рис. 9.3 и комплексным величинам ![]() в (9.2).
в (9.2).
Выбрав масштабы ![]() , отложим векторы
, отложим векторы ![]() (рис. 9.6). Конец вектора
(рис. 9.6). Конец вектора ![]() примем за начало
примем за начало ![]() для построения круговой диаграммы тока
для построения круговой диаграммы тока ![]() .
.
Вычислим ток ![]() при коротком замыкании изменяющегося сопротивления, т. е. при
при коротком замыкании изменяющегося сопротивления, т. е. при ![]() , получим
, получим ![]() . Ток
. Ток ![]() совпадает по фазе с напряжением
совпадает по фазе с напряжением ![]() . Отложив вектор
. Отложив вектор ![]() из конца вектора
из конца вектора ![]() получим хорду
получим хорду ![]() круговой диаграммы тока
круговой диаграммы тока ![]() . Выбрав масштаб
. Выбрав масштаб ![]() , отложим отрезок
, отложим отрезок ![]() Затем из точки А под углом
Затем из точки А под углом ![]() проведем линию изменяющегося параметра AN’. Перпендикуляр
проведем линию изменяющегося параметра AN’. Перпендикуляр ![]() , проведенный из начала диаграммы
, проведенный из начала диаграммы ![]() к линии изменяющегося параметра AN’, совпадает с хордой
к линии изменяющегося параметра AN’, совпадает с хордой ![]() . Поэтому перпендикуляр, восстановленный из середины хорды
. Поэтому перпендикуляр, восстановленный из середины хорды ![]() (показан штриховой линией), пересекается с
(показан штриховой линией), пересекается с ![]() в середине хорды. Эта точка пересечения — центр С круговой диаграммы. Таким образом, в рассматриваемом случае хорда
в середине хорды. Эта точка пересечения — центр С круговой диаграммы. Таким образом, в рассматриваемом случае хорда ![]() является диаметром окружности. Круговая диаграмма тока
является диаметром окружности. Круговая диаграмма тока ![]() — это половина дуги окружности, лежащей слева от
— это половина дуги окружности, лежащей слева от ![]() (на той стороне, где находится линия изменяющегося параметра). На круговой диаграмме показано положение вектора
(на той стороне, где находится линия изменяющегося параметра). На круговой диаграмме показано положение вектора ![]() для некоторого частного значения
для некоторого частного значения ![]() . Так как
. Так как ![]() , то, как видно из построения, конец вектора
, то, как видно из построения, конец вектора ![]() перемещается по той же полуокружности, по которой перемещается конец вектора
перемещается по той же полуокружности, по которой перемещается конец вектора ![]() .
.
На диаграмме отмечены два резонансных режима (токи ![]() совпадают по фазе с напряжением
совпадают по фазе с напряжением ![]() ): первый резонансный режим
): первый резонансный режим ![]() получается при
получается при ![]() и второй
и второй ![]() — при
— при ![]() Из круговой диаграммы следует, что минимум тока
Из круговой диаграммы следует, что минимум тока ![]() получается вблизи первого резонансного режима, но не при резонансе.
получается вблизи первого резонансного режима, но не при резонансе.
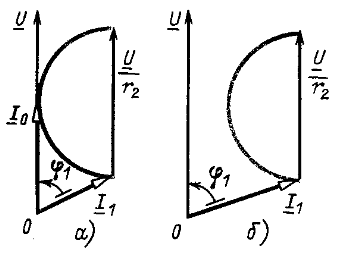
Если ![]() то круговая диаграмма расположится, как указано на рис. 9.7, а и, очевидно, возможен только один резонансный режим. При
то круговая диаграмма расположится, как указано на рис. 9.7, а и, очевидно, возможен только один резонансный режим. При ![]() (рис. 9.7, б) резонанс не получается ни при каком значении емкости С.
(рис. 9.7, б) резонанс не получается ни при каком значении емкости С.
Рис. 9.5
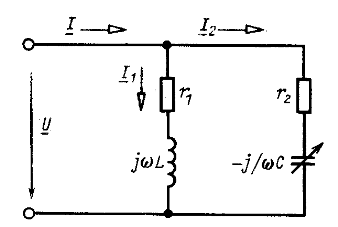
Рис. 9.6
Рис. 9.7