Несинусоидальные кривые с периодической огибающей

Кроме несинусоидальных периодических функций, разлагаемых в тригонометрический ряд на гармонические составляющие с частотами, кратными основной частоте, в электротехнике встречаются несинусоидальные кривые с периодическими или почти периодическими огибающими (см. раздел), также разлагаемые на гармонические составляющие.
Период напряжений или токов, описываемых такими кривыми, обычно во много раз превышает период любой из составляющих и может стремиться к бесконечности. К числу явлений, характеризуемых такими кривыми, относятся биения и модуляция.

Биения. Простейший случай биений получается в результате сложения двух синусоид с равными амплитудами и близкими, но не равными частотами и , причем :

Преобразуя сумму синусов, получаем

Будем считать, что кривая представляет собой синусоиду с угловой частотой , амплитуда которой изменяется по косинусоиде со значительно меньшей угловой частотой

Частотой биений называется частота , равная числу максимумов огибающей кривой в единицу времени (рис. 12.9).
Период биений в общем случае не равен периоду кривой . Действительно,

Очевидно, что только при (целое нечетное число) период биений совпадает с периодом кривой . Во всех остальных случаях кривая на участках двух соседних периодов биений не повторяется и период кривой превышает период биений. При несоизмеримости угловых частот ω и Ω их отношение является иррациональным числом, т. е. не существует такой частоты, на которую без остатка делятся частоты ω и Ω. Следовательно, период функции равен бесконечности и кривая не периодическая, хотя она и разлагается на две синусоиды.

Модулированные колебания. Синусоидально (гармонически) изменяющаяся величина задается тремя параметрами: амплитудной , угловой частотой ω и начальной фазой ψ. Все эти величины постоянны и не зависят от времени.
Однако для передачи различного рода сигналов применяются генераторы, в которых одна из этих величин сравнительно медленно изменяется по некоторому заданному закону. Изменение во времени одного из параметров называют модуляцией. Изменение амплитуды называется амплитудной модуляцией, изменение частоты ω — частотной модуляцией, изменение начальной фазы ψ — фазовой модуляцией (последние два вида модуляции не рассмотрены).
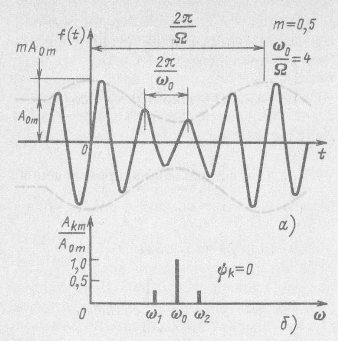
Рассмотрим простейший пример функции, изменяющейся с частотой и с амплитудой , модулированной гармоническим сигналом с частотой относительно среднего значения , т. е. с законом изменения (рис. 12.10, а):

Частота называется несущей частотой, частота Ω — модулирующей частотой, а m — коэффициентом модуляции. Коэффициент модуляции характеризует степень отличия максимальной и минимальной амплитуд от среднего значения . Обычно m меньше единицы.
Амплитудная модуляция широко применяется в радиовещании и радиосвязи, где несущая частота — это частота радиосвязи, а модулирующей Ω служит, например, одна из звуковых частот передаваемой речи или музыки.
При определении токов или напряжений в цепях, схемы которых содержат источники ЭДС, модулированных по амплитуде, последние могут быть разложены на синусоидальные составляющие. Действительно, после преобразования произведения
в выражении (12.27) получим

Рис. 12.9

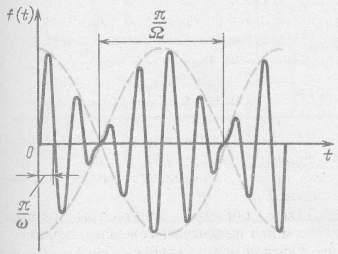
Рис. 12.10

где и начальная фаза каждой из трех гармонических составляющих .
Таким образом, простейшие модулированные по амплитуде колебания могут быть представлены в виде суммы трех синусоидальных колебаний с несущей частотой , боковыми частотами и постоянными амплитудами.
Дискретный спектр амплитуд функции (12.28) представлен на рис. 12.10, б.
При иррациональности отношения несущей и модулирующей Ω частот они несоизмеримы, а следовательно, кривая f(t) не периодическая. Тем не менее эта кривая совершенно точно может быть представлена в виде суммы трех синусоидальных составляющих различных частот.

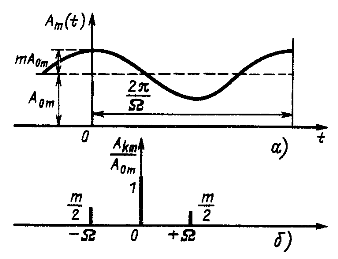
Представляет интерес сопоставить спектр модулированных колебаний со спектром огибающей колебаний (рис. 12.11,а). Спектр огибающей содержит постоянную составляющую и 1-ю гармонику с амплитудой . Учитывая, что , запишем огибающую (по аналогии с примером 12.2) в виде

и представим спектр в виде трех спектральных линий: на нулевой частоте (постоянная составляющая) и на частотах —Ω и Ω, расположенных симметрично относительно постоянной составляющей (рис. 12.11, б). Сопоставляя спектр модулированных колебаний (рис. 12.10, б) и симметричный спектр огибающей , легко заметить, что они отличаются только сдвигом по оси частот на интервал, равный несущей частоте .
Это соотношение между частотными спектрами огибающей и модулированных колебаний имеет большое значение, когда рассматривают различные случаи амплитудной модуляции.

Рис. 12.11

Модулированные импульсы. Передача сигналов может производиться как при помощи изменения параметров синусоиды, так и путем изменения параметров последовательности импульсов (см. пример 12.3).
Изменение во времени амплитуды импульсов носит название амплитудно-импульсной модуляции (АИМ), изменение продолжительности импульсов τ — широтно-импульсной модуляции (ШИМ), изменение частоты импульсов — частотно-импульсной модуляции (ЧИМ), а изменение фазы импульсов — фазо-импульсной модуляции (ФИМ).
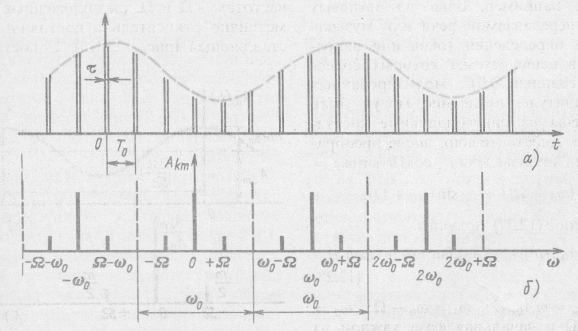
Рассмотрим простейший пример амплитудно-импульсной модуляции при (см. пример 12.4), если амплитуда импульсов изменяется во времени (рис. 12.12, а) по закону

Согласно (12.12а) спектр модулированных импульсов приближенно описывается уравнением

После преобразования произведения косинусов получим

Таким образом, спектр модулированных импульсов (рис. 12.12, б) представляет собой периодическую функцию, повторяющую с периодом симметричный спектр модулирующей огибающей (рис. 12.11, б). Чтобы спектр модулированных колебаний на каждом из интервалов частот без искажений воспроизводил спектр модулирующей огибающей, необходимо выполнить условие .
Это очень важное в практике радиотехники, телемеханики и автоматики неравенство было получено акад. В. А. Котельниковым.