Последовательное соединение приемников при синусоидальных токах
При последовательном соединении n приемников энергии с комплексными сопротивлениями ![]() эквивалентное или общее комплексное сопротивление цепи
эквивалентное или общее комплексное сопротивление цепи![]()
причем![]()
Порядок расчета цепи с последовательным соединением элементов зависит от того, какие величины заданы и какие нужно найти.
Пример 4.1.
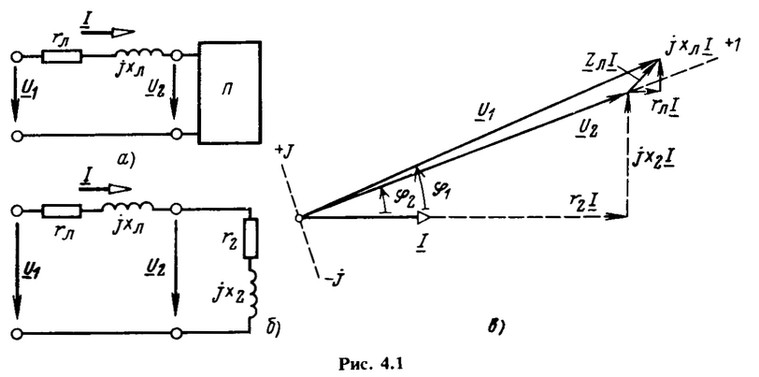
На рис. 4.1, а показана схема замещения линии электропередачи с присоединенным к ней приемником. Линия представлена последовательным соединением резистивного и реактивного элементов с сопротивлениями ![]() , а приемник — пассивным двухполюсником. Индексами 1 и 2 обозначены величины, относящиеся соответственно к началу и концу линии.
, а приемник — пассивным двухполюсником. Индексами 1 и 2 обозначены величины, относящиеся соответственно к началу и концу линии.
Дано: ![]()
Определить напряжение в начале линии ![]() .
.
Решение.
Представим пассивный двухполюсник эквивалентной схемой, состоящей из последовательного соединения элементов ![]() (рис. 4.1, б).
(рис. 4.1, б).
Ток в двухполюснике (и в линии) ![]()
Сопротивления
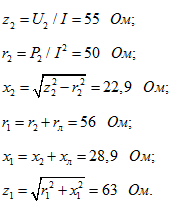
Искомое напряжение ![]() .
.
На рис. 4.1, в показана векторная диаграмма напряжений и тока (заметим, что в курсе электрических сетей приводятся удобные для расчета формулы, позволяющие просто определять разность ![]() и находить
и находить ![]() ).
).
Пример 4.2.
Для той же цепи, что и в примере 4.1, дано:![]() Определить
Определить ![]() .
.
Решение.
Сопротивление ![]() . Сопротивление
. Сопротивление ![]() определяется по аналогичной формуле, но предварительно надо найти
определяется по аналогичной формуле, но предварительно надо найти ![]()
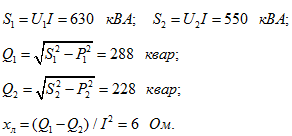
Пример 4.3.
Для той же цепи, что и в примере 4.1, дано: ![]()
Определить ток в линии I.
Решение.
Для решения задачи составим уравнение
![]()
Примем начальную фазу напряжения ![]() Начальная фаза тока
Начальная фаза тока ![]() и, следовательно,
и, следовательно, ![]() . Комплексное напряжение
. Комплексное напряжение ![]() .
.
Подставим в уравнение (а) известные величины
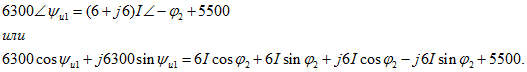
Из этого уравнения с комплексными величинами получаем два уравнения (для действительных и мнимых величин):
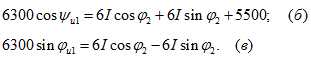
Эти два уравнения с геометрической точки зрения представляют равенства проекций вектора ![]() суммам проекций векторов
суммам проекций векторов ![]() на две взаимно перпендикулярные оси (ось действительных и ось мнимых величин).
на две взаимно перпендикулярные оси (ось действительных и ось мнимых величин).
Находим:![]()
Подставив значение ![]() в уравнения (б) и (в), получим
в уравнения (б) и (в), получим