Частотные характеристики параллельного контура
Построим резонансную кривую тока ![]() в неразветвленной части параллельного контура при неизменном напряжении U источника питания для идеального случая
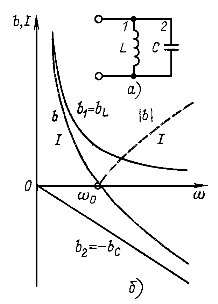
в неразветвленной части параллельного контура при неизменном напряжении U источника питания для идеального случая ![]() (рис. 5.8, а).
(рис. 5.8, а).
На рис. 5.8, б показаны частотные характеристики проводимостей ветвей ![]() и
и ![]() и входной проводимости цепи
и входной проводимости цепи ![]() . Ток
. Ток ![]() , поэтому кривая
, поэтому кривая ![]() в соответствующем масштабе и есть резонансная кривая тока
в соответствующем масштабе и есть резонансная кривая тока ![]() .
.
При изменении частоты от 0 до ![]() эквивалентная проводимость b > 0, т. е. индуктивная, и изменяется от
эквивалентная проводимость b > 0, т. е. индуктивная, и изменяется от ![]() до 0. При
до 0. При ![]() наступает резонанс токов,
наступает резонанс токов, ![]() и
и ![]() , При возрастании частоты от
, При возрастании частоты от ![]() до
до ![]() входная проводимость b < 0, т. е. емкостная и изменяется от 0 до
входная проводимость b < 0, т. е. емкостная и изменяется от 0 до ![]() .
.
В общем случае при сопротивлениях ![]() и
и ![]() , не равных нулю (см. рис. 5.5), входная активная проводимость цепи отлична от нуля при любой частоте, поэтому ток I ни при одном значении частоты не равен нулю. Анализ, который здесь не приводится, показывает, что при условии
, не равных нулю (см. рис. 5.5), входная активная проводимость цепи отлична от нуля при любой частоте, поэтому ток I ни при одном значении частоты не равен нулю. Анализ, который здесь не приводится, показывает, что при условии ![]() и
и ![]() зависимость
зависимость ![]() при U = const имеет минимум, причем этот минимум наблюдается при частоте, отличающейся от резонансной частоты. Последнее объясняется тем, что максимум полного входного сопротивления получается при частоте, для которой
при U = const имеет минимум, причем этот минимум наблюдается при частоте, отличающейся от резонансной частоты. Последнее объясняется тем, что максимум полного входного сопротивления получается при частоте, для которой ![]() , а резонанс имеет место при частоте, для которой b=0 или x= 0. Чем меньше
, а резонанс имеет место при частоте, для которой b=0 или x= 0. Чем меньше ![]() и
и ![]() , тем меньше минимальное значение тока I, тем ближе значение частоты, при которой наблюдается минимум тока, к резонансной частоте и тем меньше резонансная кривая тока отличается от кривой
, тем меньше минимальное значение тока I, тем ближе значение частоты, при которой наблюдается минимум тока, к резонансной частоте и тем меньше резонансная кривая тока отличается от кривой ![]() при
при ![]() (рис. 5.8).
(рис. 5.8).
При условии ![]() и U = const ток I, как было показано в разделе, при любой частоте одинаков. Зависимость
и U = const ток I, как было показано в разделе, при любой частоте одинаков. Зависимость ![]() не имеет ни максимума, ни минимума и графически представляется прямой, параллельной оси абсцисс.
не имеет ни максимума, ни минимума и графически представляется прямой, параллельной оси абсцисс.
Анализ показывает, что при условии ![]() и
и ![]() резонансная кривая тока при некотором значении частоты достигает максимума.
резонансная кривая тока при некотором значении частоты достигает максимума.
Рис. 5.8
Резонансные явления в электрических сетях
Вынужденные и свободные колебания
Резонанс в последовательном контуре
Частотные характеристики и резонансные кривые последовательного контура
Резонансные явления при изменении параметров контура
Резонанс в параллельном контуре
Частотные характеристики параллельного контура
Понятие о резонансе в сложных цепях