Трансформаторные подстанции высочайшего качества

Если к выводам симметричной трехфазной цепи приложена симметричная система напряжений прямой, обратной или нулевой последовательностей, то в цепи возникает симметричная система токов соответственно той же самой последовательности, какую имеют приложенные напряжения. Отношения приложенных комплексных фазных напряжений прямой, обратной и нулевой последовательностей к соответствующим комплексным фазным токам называют соответственно комплексными сопротивлениями цепи прямой (Z₁, обратной (Z₂) и нулевой (Z₀) последовательностей.
В любых симметричных трехфазных статических цепях (цепях, не содержащих вращающихся машин) изменение порядка следования фаз приложенных симметричных напряжений с прямого на обратный не изменяет значения токов (изменяется только их последовательность с прямой на обратную). Поэтому для таких цепей сопротивления прямой и обратной последовательностей одинаковы (Z₁ = Z₂).

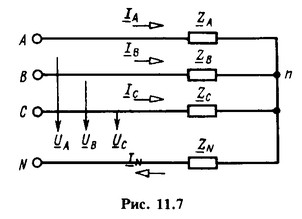Рассмотрим, например, трехфазную симметричную цепь (рис. 11.7), в которой . Очевидно, что для этой цепи .
Определим для нее .
Пусть к выводам цепи приложена симметричная система фазных напряжений нулевой последовательности . при этом система токов также симметрична и имеет нулевую последовательность . Ток в нейтральном проводе .
Составим для контура AnNA уравнение

и, подставив и , получим , откуда

При отсутствии нейтрального провода токи нулевой последовательности протекать не могут: .
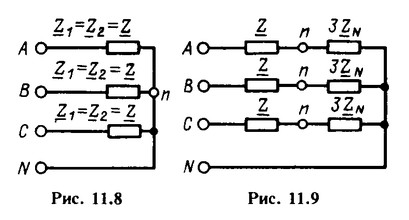
При расчетах цепей методом симметричных составляющих рассматривают отдельно схемы для токов и напряжений различных последовательностей. Сопротивление в нейтральном проводе не оказывает влияния на симметричные системы токов прямой и обратной последовательностей, поэтому в схемах для токов этих последовательностей сопротивления в нейтральном проводе не указывают (рис. 11.8). В схеме для симметричных токов и напряжений нулевой последовательности вместо сопротивления в нейтральном проводе вводят утроенные значения этого сопротивления в каждую фазу (рис. 11.9). Легко проверить, что сопротивления нулевой последовательности для схем, представленных на рис. 11.7 и 11.9, одинаковы.

Все расчеты ведут для одной фазы, которую называют основной. Обычно за основную фазу принимают фазу А, и в этом случае для сокращения записи в обозначениях токов и напряжений различных последовательностей индекс А не пишут. Так, для рассматриваемого примера (см. рис. 11.7) на рис. 11.10 показаны три однофазные схемы для токов и напряжений различных последовательностей. Эти схемы сокращенно называются схемами прямой, обратной и нулевой последовательностей.
В качестве схем прямой и обратной последовательностей для трехфазных линий можно применять любую из двух схем, показанных на рис. 30 и 31. В схему нулевой последовательности должны быть введены утроенные значения сопротивления г, и индуктивности М (см. рис. 29) в каждую фазу. В зависимости от того, разнесены частичные емкости поровну по концам линии или сосредоточены в середине, получатся две разновидности схем нулевой последовательности для трехфазной линии, не отличающиеся по структуре от схем, показанных на рис. 30 и 31. Только в этих схемах вместо следует взять (через частичные емкости токи нулевой последовательности протекать не могут).
В электрических машинах не только отличается от , но .
Причину этого поясним на примере асинхронного двигателя. В нормальном режиме работы к обмоткам статора двигателя приложена симметричная система напряжений прямой последовательности, магнитное поле и ротор двигателя вращаются в одну и ту же сторону (см. раздел). Частота вращения ротора обычно всего на 1,5 — 4% меньше частоты вращения магнитного поля. Иные условия получаются в симметричном режиме для токов и напряжений обратной последовательности. Обеспечим вращение ротора двигателя с той же скоростью и в том же направлении, какие были в нормальном режиме работы (например, вращая его посредством другого двигателя), но изменим последовательность фаз напряжений, подведенных к обмоткам статора, с прямой на обратную. При этом в обмотках двигателя будет симметричная система токов обратной последовательности, которая создаст магнитное поле, вращающееся с той же скоростью, как и в нормальном режиме работы, но только в обратную сторону (навстречу движению ротора). В результате вращающееся магнитное поле относительно ротора будет иметь скорость, почти в 2 раза превышающую скорость движения поля относительно статора и во много раз превышающую скорость поля относительно ротора при нормальном режиме работы. По сравнению с нормальным режимом резко возрастут токи, индуктированные в роторе. По закону Ленца они будут ослаблять наводящее их магнитное поле в большей мере, чем в условиях нормального режима. Это приведет к уменьшению ЭДС, наводимых магнитным полем в обмотках статора. А так как приложенные к обмоткам статора напряжения в основном уравновешиваются этими ЭДС, то их уменьшение вызовет увеличение токов в статоре.
Таким образом, при одинаковых значениях приложенных симметричных напряжений прямой и обратной последовательностей и при неизменных частоте и направлении вращения ротора токи обратной последовательности получаются больше токов прямой последовательности. Следовательно, полное сопротивление двигателя для токов обратной последовательности меньше его сопротивления для токов прямой последовательности: .
Токи нулевой последовательности не создают вращающегося магнитного поля (для получения движущегося магнитного поля, как было указано в разделе, нужно иметь не только пространственно смещенные обмотки, но и сдвинутые по фазе токи в них). Значит, условия протекания в двигателе токов нулевой последовательности отличаются от условий протекания токов прямой и обратной последовательностей, поэтому .
В расчетах методом симметричных составляющих двигатели, как и статические цепи, представляют тремя отдельными схемами прямой, обратной и нулевой последовательностей, состоящими соответственно из сопротивлений . Генераторы имеют такие же схемы, но с тем отличием, что в схеме прямой последовательности кроме сопротивлений включены источники фазных ЭДС.
Отметим, что неравенство сопротивлений приводит к тому, что трехфазные цепи, содержащие вращающиеся машины, не обладают свойством взаимности.