Трансформаторные подстанции высочайшего качества

Для ознакомления с расчетами симметричных режимов рассмотрим порядок расчета токов в симметричной цепи рис. 13. Пусть напряжения на выводах источника питания симметричны и заданы и пусть известны сопротивления всех элементов цепи 1, 2, 3 и 4. Для выполнения расчета проще всего преобразовать схему, заменив соединения треугольниками источника питания и элементов 4 на соединении звездами. Сопротивления фаз симметричной звезды в 3 раза меньше сопротивлений фаз эквивалентного симметричного треугольника. Фазные напряжения эквивалентного источника питания, соединенного звездой, в раз меньше заданных линейных напряжений. Таким образом, получается схема, показанная на рис. 14.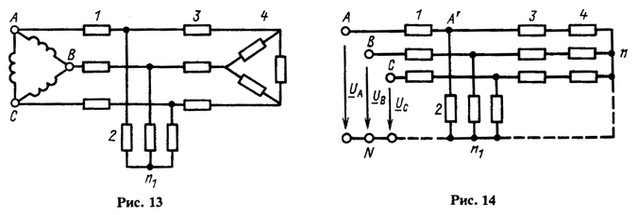

Все нейтральные точки в симметричном режиме имеют одинаковый потенциал. Поэтому, не нарушая режима, соединим их проводом без сопротивления (показан штриховой линией). Затем удалим из схемы две фазы, например В и С, и перейдем к схеме на рис. 15. Это не изменит режима оставшейся фазы А.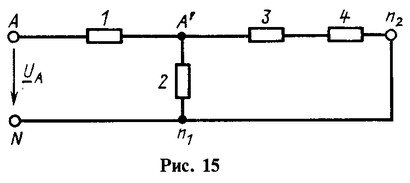

Действительно, уравнения, составленные по законам Кирхгофа, для узла А’ и для контуров AA’n1N и А’n2n1А’ для схем, показанных на рис. 14 и 15, одинаковы, а следовательно, токи и напряжения в фазе А обеих схем также одинаковы. Токи в фазе А легко рассчитываются по однофазной схеме (рис. 15), например, методом ее дальнейшего преобразования — заменой параллельного соединения ветвей А’n2 и А’n1 эквивалентным сопротивлением. Токи в фазах В и С по модулю такие же, что и в фазе А. Токи в ветвях треугольника 4 в раз меньше токов в элементах 3 (в каждом из элементов любой из групп ток сдвинут по фазе по отношению к токам в других элементах той же группы на равные углы + 120°).
Для расчета симметричных режимов в сложных разветвленных трехфазных цепях широко применяют моделирование соответствующих однофазных схем.