Применение топологических уравнений для построения сигнальных графов

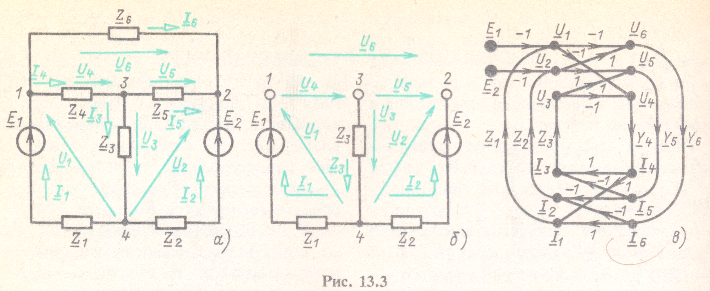
Для построения графа на основании законов Кирхгофа следует придерживаться определенной последовательности. Сначала выбирается дерево, содержащее ветви с источниками ЭДС или без источников ЭДС, но не содержащее источников тока. Так, для построения графа схемы рис. 13.3, а на рис. 13.3, б выбрано дерево из трех ветвей с произвольными положительными направлениями напряжений . Затем напряжения ветвей связи выражаются через напряжения ветвей дерева, а токи ветвей дерева — через токи ветвей связи; в результате получаются уравнения

токи ветвей связи

и токи ветвей дерева

Наконец, напряжения на ветвях дерева выражаются через сопротивления, токи и ЭДС ветвей:

Последовательность построения узлов и ветвей графа соответствует последовательности записи уравнений (13.4) — (13.7). На рис. 13.3, в изображен граф для заданной мостовой схемы, полностью удовлетворяющей приведенным системам уравнений.
Если в схеме есть ветви, содержащие только идеальные источники ЭДС, и есть ветви, содержащие только идеальные источники тока, то первые должны быть включены в дерево, а вторые — в ветви связи.
Для иллюстрации построения графов методом узловых потенциалов и методом контурных токов выберем схему, показанную на рис. 13.4, а.
Пользуясь методом узловых потенциалов, записываем для этой схемы уравнения

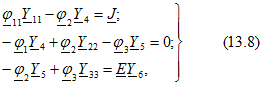
где .
Из (13.8) потенциалы узлов

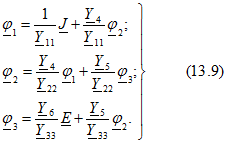
Уравнениям (13.9) удовлетворяет граф, показанный на рис. 13.4, б.
Пользуясь методом контурных токов, записываем для схемы рис. 13.4, а уравнения

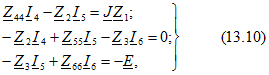
где
Из этих уравнений контурные токи

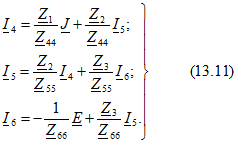
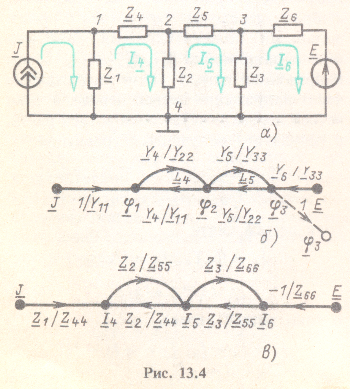
На рис. 13.4, в построен граф, удовлетворяющий (13.11).
Таким образом, в зависимости от выбранного метода расчета и составления уравнений получаются различные графы для одной и той же схемы. При этом легко убедиться, что графы, построенные на основании законов Кирхгофа, сложней графов, построенных на основании уравнений для контурных токов или узловых потенциалов.

Преобразования графов и их связь с преобразованиями электрических схем.

Для получения правил преобразования графов рассмотрим ряд примеров.
Исключим из системы уравнений (13.2) ток , а из системы уравнений (13.3) потенциал ; в результате после элементарных преобразований получим

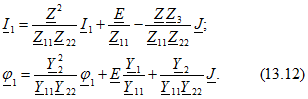
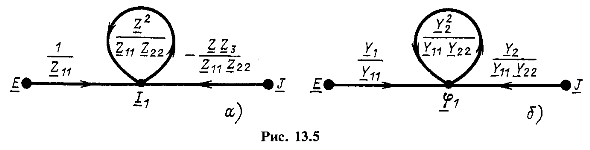
Полученным уравнениям соответствуют графы, показанные на рис. 13.5. Из сравнения первых из уравнений (13.2) и (13.12), а также из сопоставления графа, приведенного на рис. 13.1, б, с графом, показанным на рис. 13.5, а, следует, что операция исключения контурного тока из системы контурных уравнений приводит к устранению контура в заданной схеме (рис. 13.1, а) и узла с током в графе на рис. 13.1, б. В результате исключения этого узла получается в графе на рис. 13.5, а простейший контур, состоящий из петли с передачей, равной произведению передач ветвей , и ветви от источника тока с передачей, равной произведению передач ветвей . Исключение потенциала в графе на рис. 13.1, в приводит к аналогичному результату, что непосредственно следует из сравнения графов на рис. 13.1, в и рис. 13.5, б.

Таким образом, решению уравнений методом последовательного исключения неизвестных величин соответствует преобразование графа. Такие простейшие преобразования уравнений и графов показаны в табл. 13.1. Исключение неизвестных из системы уравнений автоматически приводит к исключению соответствующих узлов в графе.

Например, исключив из системы уравнений (13.8) или (13.9) для схемы рис. 13.4, а и графа, показанного на рис. 13.4, б, потенциал получим

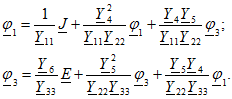
Этим уравнениям соответствует граф, изображенный на рис. 13.6, не имеющий узла с потенциалом . При этом исключение второго узла привело к тому, что в узлах с потенциалами появились петли с передачами, равными произведениям передач ветвей, которые непосредственно примыкают к первому и третьему узлам, а также изменились передачи ветвей между узлами .

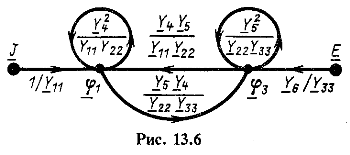
Таблица 13.1. Простейшие преобразования графов
Заданный граф	Эквивалентный граф	Уравнения преобразования графа

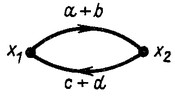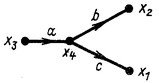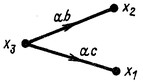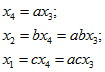Прежде чем перейти к расчету режимов в линейных цепях при помощи графов, необходимо дать определения пути, передачи пути, контура, передачи контура, определителя и минора прямого пути сигнального графа.
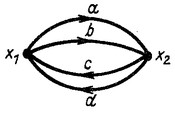
Путь — непрерывная последовательность ветвей (в указанном направлении) между двумя узлами, вдоль которой каждый узел и каждая ветвь в этой последовательности встречаются не более 1 раза; прямой путь — путь, начинающийся в истоке и заканчивающийся в стоке; передача пути П -произведение передач ветвей вдоль этого пути (имеющего определенное направление); контур — замкнутый путь (имеющий определенное направление), который начинается и заканчивается в одном и том же узле и вдоль которого любой другой узел этого контура и любая ветвь этого контура встречаются не более одного раза (в частном случае контур может состоять из одной ветви — петли); передача контура L — произведение передач ветвей этого контура; определитель графа D — определитель системы уравнений, для которой построен граф; минор прямого пути D’ — определитель части графа, получающейся из исходного при исключении ветвей прямого пути и ветвей, имеющих общие узлы с ветвями прямого пути (определитель части графа, не соприкасающийся с прямым путем).
В приведенных выше примерах были показаны некоторые преобразования графов, вытекающие преимущественно из простых преобразований системы контурных и узловых уравнений схемы. Поскольку метод графов может быть применен для анализа и других систем (не электрических), то рассмотрим еще один случай преобразования в более общей форме.
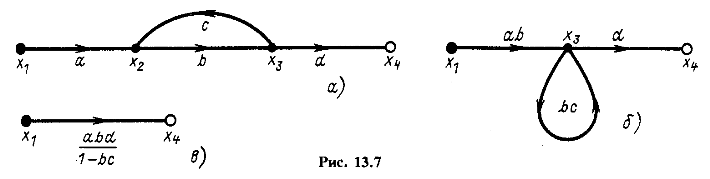
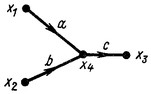
На рис. 13.7, а изображен граф с четырьмя ветвями и одним контуром, истоком и стоком . Исключая из этого графа узел с сигналом при помощи равенства , получаем для узлов уравнения

Этим уравнениям соответствует граф, приведенный на рис. 13.7, б. После подстановки значения из первого уравнения системы (13.13) во второе определяется сигнал

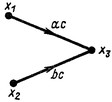
Таким образом, исключение петли приводит к графу (рис. 13.7, в) с одной ветвью, передача которой равна , где произведение abd равно передаче пути между узлами с сигналами , а произведение bс равно передаче контура L.