Коэффициенты четырехполюсников

Коэффициенты уравнений (8.1) -(8.6) постоянны (при заданной частоте) и определяются только структурой четырехполюсника и параметрами составляющих его элементов, а не параметрами источника питания и приемника. С точки зрения режима на первичных и вторичных выводах четырехполюсники, имеющие одинаковые значения коэффициентов, неотличимы, т. е. эквивалентны, хотя их внутренняя структура может быть совсем различной.
Таким образом, можно утверждать, что четырехполюсник задан, если известны его коэффициенты.
Уравнения четырехполюсника (8.1) — (8.6) показывают, что проходной активный неавтономный или пассивный четырехполюсник задается четырьмя коэффициентами любого из типов уравнений. Поэтому матрица коэффициентов одного из типов уравнений может быть выражена через матрицу коэффициентов любого другого типа уравнений.
Определим, например, связь коэффициентов уравнений типа Y с коэффициентами уравнений типа Z, выразив токи из (8.3)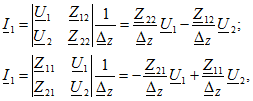

где

Из сравнения полученных уравнений с (8.2) следует, что
В табл. 8.1 приведены формулы связи коэффициентов всех систем уравнений. Коэффициенты уравнений четырехполюсника называют еще его первичными параметрами.

Каждый из первичных параметров имеет простой физический смысл. Например, по (8.3) при (в режиме холостого хода на вторичных выводах), т. е. — входное сопротивление, измеренное на первичных выводах при разомкнутых вторичных; по (8.2) при , т. е. — входная проводимость со стороны вторичных выводов при коротком замыкании первичных; по (8.4) при , т. е. и т. д.
Если известны схема четырехполюсника и значения составляющих его элементов, то любой из коэффициентов может быть определен расчетом.

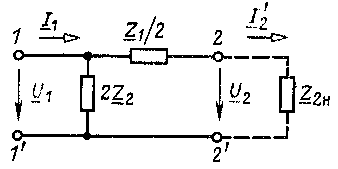
Пример 8.1. Определить коэффициенты уравнений типа А и передаточную функцию для пассивного четырехполюсника по рис. 8.5.
Решение. Выразим напряжение и ток через напряжение и ток при помощи уравнений Кирхгофа:

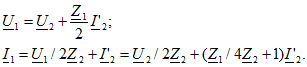
Сравнив эти зависимости с уравнениями типа А (8.1), найдем

Передаточная функция определяется после подстановки во второе уравнение (8.1а) , откуда .

Рис. 8.5

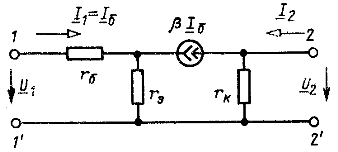
Пример 8.2. На рис. 8.6 представлена эквивалентная схема однокаскадного усилителя с транзистором, включенным по схеме с общим эмиттером. Заданы сопротивления — базы, — эмиттера, — коллектора и коэффициент b передачи тока базы (). Составить матрицу Z-параметров.
Решение. Режим неавтономного активного четырехполюсника по рис. 8.6 описывается уравнениями

Сравнив эти зависимости с уравнениями типа Z (8.3), найдем

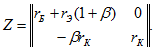
Рис. 8.6

Пассивные четырехполюсники.
Для пассивных четырехполюсников выполняется принцип взаимности и число независимых коэффициентов каждого типа уравнений уменьшается до трех.
В качестве примера найдем зависимость между коэффициентами матрицы Y. Предположим, что выходные выводы четырехполюсника замыкаются накоротко сначала при питании со стороны первичных выводов, а затем со стороны вторичных. В первом случае (см. рис. 8.3, а) и из второго уравнения типа Y получим , во втором случае (см. рис. 8.3, б) и из первого уравнения типа Y имеем . Если выбрать напряжение во втором случае равным напряжению в первом, то из принципа взаимности следует, что . Это равенство выполняется при условии

Полученный результат не является неожиданным. Коэффициенты — это по сути дела взаимные (передаточные) проводимости выходной и входной ветвей четырехполюсника при источниках ЭДС , подключенных соответственно к первичным и вторичным выводам.
При помощи табл. 8.1 или непосредственно можно найти зависимости между коэффициентами каждой из матриц

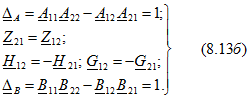
В примере 8.1 были определены коэффициенты уравнений типа А самого простого пассивного несимметричного четырехполюсника по рис. 8.5, который называется Г-образным. Нетрудно убедиться, что условие выполняется. В примере 8.2 составлена матрица Z-параметров активного неавтономного четырехполюсника. Условие для этого четырехполюсника не выполняется, как и должно быть.

Симметричный четырехполюсник.
Четырехполюсник, у которого при взаимной замене первичных и вторичных выводов режимы источника питания и приемника не изменяются, называется симметричным. У такого активного неавтономного четырехполюсника не четыре, а три независимых коэффициента (первичных или основных параметров), а у пассивного два. Например, как было показано выше, при питании четырехполюсника со стороны первичных выводов и разомкнутых вторичных При питании со стороны вторичных выводов и разомкнутых первичных у симметричного четырехполюсника должно быть такое же входное сопротивление Из уравнений (8.3) при получаем , и, следовательно,

Такие же рассуждения приводят к равенствам

Если два Г-образных четырехполюсника (см. рис. 8.5) соединить соответственно друг с другом выводами 1 и 1‘, то получится симметричный Т-образный четырехполюсник (рис. 8.7, а), а при соединении выводами 2 и 2′ — симметричный П-образный (рис. 8.7, б) — две канонические схемы пассивных симметричных четырехполюсников, которые содержат минимально возможное число двухполюсников (элементов).

Рис. 8.7

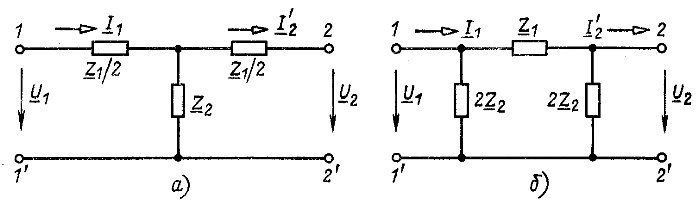
Пример 8.3. Найти коэффициенты уравнений типа А симметричного Т-образного четырехполюсника (рис. 8.7, а).
Решение. Коэффициенты могут быть найдены тем же методом, что и в примере 8.1. Однако для рассматриваемого четырехполюсника (как и многих других) вычисления упрощаются при выполнении мысленных опытов холостого хода и короткого замыкания.
При холостом ходе на вторичных выводах () из рис. 8.7, а следует, что или . Сравнив эти выражения с уравнениями (8.1а) при , определим

При коротком замыкании вторичных выводов () из рис. 8.7, а следует, что или

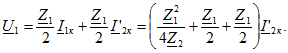
Сравнив эти выражения с уравнениями (8.1а) при , найдем

т.е. как и должно быть у симметричного четырехполюсника (8.7).

Пример 8.4. Найти коэффициенты матрицы Y для П-образного симметричного четырехполюсника (рис. 8.7, б).
Решение. Для пассивного симметричного четырехполюсника должны выполняться условия (8.13) и (8.14). Поэтому запишем уравнения (8.2) в виде

В частности, при коротком замыкании вторичных выводов

Для четырехполюсника по рис. 8.7, б

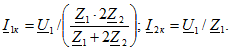
Следовательно,

Из последних двух формул можно найти параметры при заданной матрице Y:

Для симметричного пассивного четырехполюсника должны выполняться и условия (8.13), и условия (8.14), т. е., как было указано, остается два независимых параметра. Например, для симметричного Т-образного четырехполюсника (рис. 8.7, а) в примере 8.3 получено и, как нетрудно убедиться, (см. таблицу).

Коэффициенты и параметры симметричных четырехполюсников

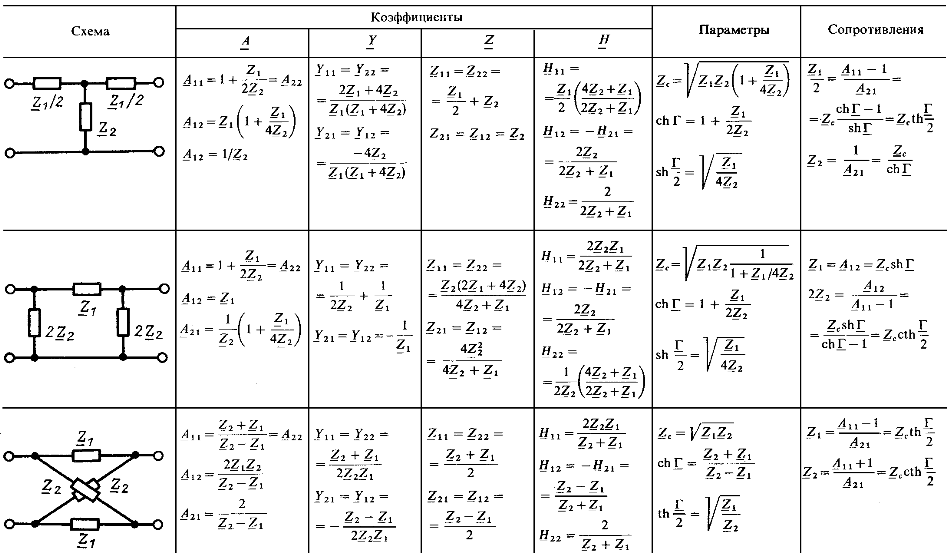
Экспериментальное определение коэффициентов и входных сопротивлений.
Первичные параметры каждого данного четырехполюсника могут быть определены экспериментально при измерении режима (напряжений и токов) на первичных и вторичных выводах. Например, при питании четырехполюсника со стороны первичных выводов (напряжение ) и холостом ходе на вторичных (напряжение токи ) из (8.1а) находим

а при коротком замыкании вторичных (напряжение , токи )

При работе четырехполюсника в цепи постоянного тока для вычисления коэффициентов достаточно измерить вольтметрами напряжения и амперметрами токи. В цепи синусоидального тока необходимо еще определить угол сдвига фаз между соответствующими величинами, например при определении коэффициента
С ростом частоты экспериментальное определение большинства коэффициентов становится все более трудным, так как измерение напряжений, токов и особенно сдвига фаз усложняется. У четырехполюсников — линий передачи сигналов — экспериментальное определение коэффициентов по результатам двух опытов практически вообще невозможно, так как требует включения прибора, измеряющего сдвиг фаз (ваттметр, осциллограф, фазометр), одновременно к входным и выходным выводам линии.
Сопротивления холостого хода и короткого замыкания могут быть измерены теми же методами, что и любые другие сопротивления, например при помощи измерительного моста или амперметра, вольтметра и ваттметра, включенных только со стороны первичных или только со стороны вторичных выводов. Поэтому для большинства четырехполюсников измерение сопротивлений можно выполнить точнее и проще, чем измерение коэффициентов четырехполюсника, особенно на высоких частотах.
Однако в общем случае по найденным экспериментально или расчетом сопротивлениям холостого хода и короткого замыкания нельзя определить четыре независимых коэффициента какого-либо типа уравнений. Действительно, эти сопротивления связаны соотношением (8.12), т. е. у четырехполюсника три независимых сопротивления холостого хода и короткого замыкания.
У пассивных четырехполюсников коэффициенты каждой из матриц первичных параметров связаны дополнительно условиями (8.13), т. е. число независимых коэффициентов равно трем. Поэтому коэффициенты можно выразить через сопротивления холостого хода и короткого замыкания. В качестве примера свяжем коэффициенты уравнений типа А с одной из троек независимых сопротивлений: Подставив в соотношение значения коэффициентов из (8.9) -(8.11), получим

откуда

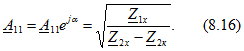
Аналогично можно получить формулы для коэффициентов Но при вычисленном уже коэффициенте (8.16) и известных сопротивлениях коэффициенты проще найти из (8.9) -(8.11).
Если задана (измерена или рассчитана) другая тройка сопротивлений, то можно пользоваться этими же выражениями, предварительно вычислив четвертое сопротивление из (8.12).
Следует обратить внимание на то, что выражение (8.16) дает два значения коэффициента При извлечении квадратного корня из комплексного числа получаются два комплекса, аргументы которых отличаются на 180° (π) или знаком минус перед модулем:

Соответственно получаются два значения и для других коэффициентов. Выбор того или иного значения коэффициента зависит от разметки вторичных выводов. После того как выбрана разметка первичных выводов, представляются две возможности при разметке вторичных: а) верхний вывод 2, нижний 2′, как на рис. 8.1, и положительное направление напряжения U_2 от 2 к 2′; б) верхний вывод 2′, нижний 2 и положительное направление напряжения опять от 2 к 2′, т. е. противоположно первому случаю.
Изменение положительного направления напряжения равносильно изменению его фазы на 180°. Такое изменение фазы и получается, если вместо первого значения коэффициента (т. е. ) выбрать второе значение (), что видно, например, из (8.15а): . При изменении разметки вторичных выводов сопротивления холостого хода и короткого замыкания остаются неизменными. Поэтому опыты холостого хода и короткого замыкания не дают возможности выбрать одно из двух значений коэффициента и т. е. провести разметку вторичных выводов.
Аналогичное замечание нужно учесть и при расчете коэффициентов уравнений других типов.