Аналитическое описание нелинейных характеристик

Характеристики нелинейных элементов обычно задаются (в результате проведения экспериментов) в виде таблиц значений аргумента и функции или в виде графиков, которыми часто иллюстрируются таблицы экспериментальных значений.
Для анализа нелинейных цепей часто необходимо иметь аналитическое описание нелинейных характеристик в виде одной или нескольких функций, определяемых для каждого из участков характеристики.
Если из физических соображений можно предложить аналитическую форму описания нелинейной функции, то входящие в эту функцию постоянные могут быть найдены по правилам аппроксимации при помощи известных математических программ, обычно основывающихся на минимизации модуля или среднеквадратичного расхождения между аналитической функцией и экспериментальными данными. Стандартные программы для решения таких задач имеются в программном обеспечении ЭВМ.
Далеко не всегда при помощи одной аналитической функции с достаточной точностью удается описать всю заданную характеристику. Более точным и универсальным методом аналитического описания нелинейной характеристики является кусочно-аналитическое описание функции на отдельных участках.
Будем считать, что характеристика задана рядом точек

Наиболее грубо аппроксимация нелинейной характеристики может быть выполнена при помощи кусочно-постоянных или кусочно-линейных функций.
В первом случае на участке эта функция постоянна, например

и полученная характеристика представляет собой ступенчатую функцию.
Во втором случае на этом участке

и полученная характеристика имеет вид ломаной линии с точками излома в заданных точках характеристики.
Более точным описанием экспериментальной зависимости является ее задание в виде совокупности отрезков квадратичных или кубических парабол, коэффициенты которых определяются из условия отсутствия разрыва производных в точках сопряжения. Метод аппроксимации экспериментальных зависимостей квадратичными полиномами называют параболическими сплайнами, а кубическими полиномами — кубическими сплайнами (от английского слова spline, что значит обшивать гибкой рейкой углы в строительных конструкциях).
Для параболического сплайна аппроксимация на участке от до выражается функцией

где коэффициенты определяются из условия непрерывности функции и ее производной в точках сопряжения:

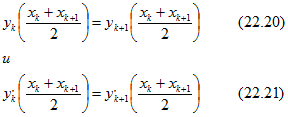
Таким образом, при n заданных точках имеется 2(n — 1) уравнений в точках сопряжения и требуется еще два дополнительных условия для однозначного определения 2n коэффициентов парабол (22.19). Обычно эти два условия задаются в виде значений первой и второй производных функции у(х) или их линейной комбинации на одном или обоих концах интервала описания функции. Поэтому они называются краевыми условиями.
При аппроксимации кубическими сплайнами узлы аппроксимации и узлы сопряжения совпадают. Поэтому для нахождения коэффициентов кубических полиномов используют условия: прохождение сплайна через узлы

равенство в узлах первых производных

равенство в узлах вторых производных

Как и в случае параболического сплайна, для однозначного определения коэффициентов необходимо задать еще два краевых условия.
Кубические сплайны выражают через значения вторых производных в узлах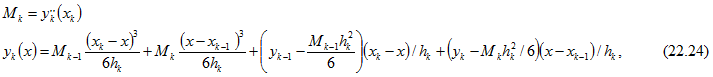

где , или через значения первых производных , т.е. наклоны нелинейных характеристик

Для определения коэффициентов или требуется решить систему n — 1 линейных уравнений

где k = 1, 2, …, n — 1;

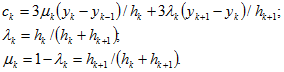
Для решения системы уравнений (22.26) дополнительно должны быть заданы краевые условия по первым производным или по вторым производным . В последнем случае система (22.26) дополняется уравнениями

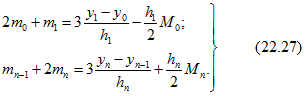
Так как объем вычислений для параболических и кубических сплайнов примерно одинаков, но последние обладают более высокой точностью и более широкими возможностями, на практике преимущественное распространение получили кубические сплайны. Можно избежать необходимости решения системы (22.26), если одновременно со значениями функции в узлах аппроксимации задавать значение первой или второй производных или вычислять эти коэффициенты по отношению .
Достоинствами сплайн-аппроксимации являются высокая гибкость и точность описания при достаточно редком расположении точек.
Таким образом, в случае применения ЭВМ нетрудно получить аналитически с необходимой точностью значение переменной у при заданном х или обратной функции х(у), так как строки х и у равноправны (см. начало параграфа).
Если известны n линейных уравнений для линейной части цепи и n нелинейных характеристик в виде аппроксимирующих функций, то решение задачи анализа или синтеза нелинейной электрической цепи может быть произведено при помощи ЭВМ по одной из стандартных программ решения системы алгебраических уравнений. В программах широко применяется метод итераций.