Расчет напряжения, потери напряжения (страница 2)
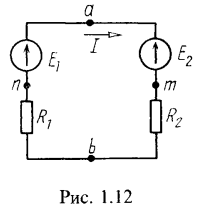
1. В неразветвленной цепи (рис. 1.12) ЭДС ![]() , сопротивления
, сопротивления ![]() . Определить напряжение между точками а и b.
. Определить напряжение между точками а и b.
Решение:
Задавшись положительным направлением тока по часовой стрелке, на основании закона Ома:
![]()
Так как результат оказался положительным, то истинное направление тока совпадает с выбранным. Напряжение между точками а и b можно найти по закону Ома, примененному к участку amb:
![]()
откуда ![]() .
.
Такой же результат можно получить, если применить ту же формулу к участку bna:
![]() или
или ![]() , а следовательно,
, а следовательно, ![]() .
.
Замечание. Если на участке цепи, содержащем ЭДС и сопротивление, ток и ЭДС совпадают по направлению, то напряжение на зажимах участка меньше ЭДС на величину падения напряжения в сопротивлении участка, а если направление тока противоположно направлению ЭДС, то напряжение на зажимах участка больше ЭДС на величину падения напряжения в рассматриваемом участке.
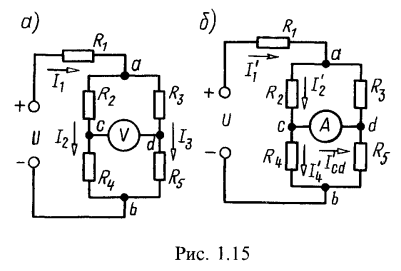
2. Определить токи в ветвях цепи (рис. 1.15, а) и показание вольтметра, включенного между точками с и d, считая, что его сопротивление во много раз превышает сопротивление каждого из элементов цепи. Чему равно показание амперметра, включенного между точками c и d, сопротивление которого считать равным нулю? Дано: ![]()
Решение:
Расчет показания вольтметра. Из условия вытекает, что его включение не оказывает влияния на распределение токов в цепи. Для расчета токов сначала определяем эквивалентное сопротивление всей цепи (рис. 1.15, а):
![]()
В неразветвленной части цепи проходит ток:
![]() .
.
Токи, проходящие через сопротивления ![]() , можно найти различными методами.
, можно найти различными методами.
1. В параллельных ветвях токи распределяются обратно пропорционально их сопротивлениям [см. формулу (0.1.19)]:
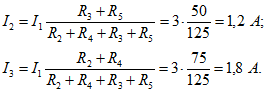
2. Найдем напряжение на зажимах параллельных ветвей:
![]()
Токи в ветвях с сопротивлениями ![]() равны
равны
![]()
Напряжение на зажимах параллельных ветвей можно найти как разность между приложенным напряжением и падением напряжения на сопротивлении ![]() .
.
Найдем показание вольтметра, равное напряжению между точками с и d:![]()
Вычислим ток, проходящий через амперметр; он равен току короткого замыкания ![]() (рис. 1.15,6). Для его нахождения вычислим токи
(рис. 1.15,6). Для его нахождения вычислим токи
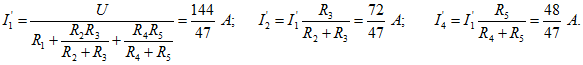
Искомый ток, проходящий через амперметр,
![]()