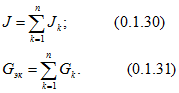Трансформаторные подстанции высочайшего качества

Цепь состоит из ветвей, имеет узлов и источников тока. Приводимые далее формулы пригодны для расчета цепей, содержащих и источники напряжения и источники тока. Они справедливы и для тех частных случаев: когда в цепи имеются только источники напряжения или только источники тока.

Применение законов Кирхгофа. Обычно в цепи известны все источники ЭДС и источники токов и все сопротивления. В этом случае устанавливается число неизвестных токов, равное . Для каждой ветви задаются положительным направлением тока.
Число У взаимонезависимых уравнений, составляемых по первому закону Кирхгофа, равно числу узлов без единицы. Число взаимонезависимых уравнений, составляемых по второму закону Кирхгофа,

При составлении уравнений по второму закону Кирхгофа следует выбирать независимые контуры, не содержащие источников тока. Общее число уравнений, составляемых по первому и по второму законам Кирхгофа, равно числу неизвестных токов.
Примеры приведены в задачах раздела.

Метод контурных токов (Максвелла). Этот метод позволяет уменьшить количество уравнений системы до числа К, определяемого формулой (0.1.10). Он основан на том, что ток в любой ветви цепи можно представить в виде алгебраической суммы контурных токов, протекающих по этой ветви. При пользовании этим методом выбирают и обозначают контурные токи (по любой ветви должен проходить хотя бы один выбранный контурный ток). Из теории известно, что общее число контурных токов . Рекомендуется выбирать контурных токов так, чтобы каждый из них проходил через один источник тока (эти контурные токи можно считать совпадающими с соответствующими токами источников тока и они обычно являются заданными условиями задачи), а оставшиеся контурных токов выбирать проходящими по ветвям, не содержащим источников тока. Для определения последних контурных токов по второму закону Кирхгофа для этих контуров составляют К уравнений в таком виде:

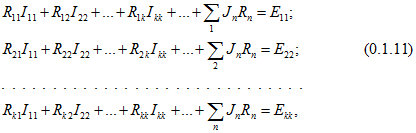
где — собственное сопротивление контура n (сумма сопротивлений всех ветвей, входящих в контур n); — общее сопротивление контуров n и l, причем , если направления контурных токов в общей ветви для контуров n и l совпадают, то положительно , в противном случае отрицательно ; — алгебраическая сумма ЭДС, включенных в ветви, образующие контур n; — общее сопротивление ветви контура n с контуром, содержащим источник тока .
Примеры приведены в задачах раздела.

Метод узловых напряжений. Этот метод позволяет уменьшить количество уравнений системы до числа У, равного количеству узлов без одного

Сущность метода заключается в том, что вначале решением системы уравнений (0.1.13) определяют потенциалы всех узлов схемы, а токи ветвей, соединяющих узлы, находят с помощью закона Ома.
При составлении уравнений по методу узловых напряжений вначале полагают равным нулю потенциал какого-либо узла (его называют базисным). Для определения потенциалов оставшихся узлов составляется следующая система уравнений:

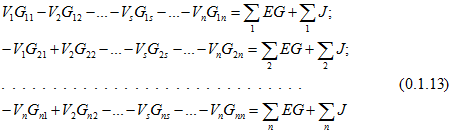
Здесь — сумма проводимостей ветвей, присоединенных к узлу s; — сумма проводимостей ветвей, непосредственно соединяющих узел s с узлом q; — алгебраическая сумма произведений ЭДС ветвей, примыкающих к узлу s, на их проводимости; при этом со знаком « + » берутся те ЭДС, которые действуют в направлении узла s, и со знаком «—» — в направлении от узла s; — алгебраическая сумма токов источников тока, присоединенных к узлу s; при этом со знаком « + » берутся те токи, которые направлены к узлу s, а со знаком « —» — в направлении от узла s.
Методом узловых напряжений рекомендуется пользоваться в тех случаях, когда число уравнений меньше числа уравнений, составленных по методу контурных токов.
Если в схеме некоторые узлы соединяются идеальными источниками ЭДС, то число У уравнений, составляемых по методу узловых напряжений, уменьшается:

где — число ветвей, содержащих только идеальные источники ЭДС.
Примеры приведены в задачах раздела.
Частный случай—двухузловая схема. Для схем, имеющих два узла (для определенности узлы а и b), узловое напряжение

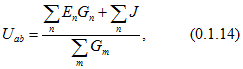
где — алгебраическая сумма произведений ЭДС ветвей (ЭДС считаются положительными, если они направлены к узлу а, и отрицательными, если от узла а к узлу b) на проводимости этих ветвей; — токи источников тока (положительны, если они направлены к узлу а, и отрицательны, если направлены от узла а к узлу b); — сумма проводимостей всех ветвей, соединяющих узлы а и b.

Принцип наложения. Если в электрической цепи заданными значениями являются ЭДС источников и токи источников тока, то расчет токов на основании принципа наложения состоит в следующем. Ток в любой ветви можно рассчитать как алгебраическую сумму токов, вызываемых в ней ЭДС каждого источника ЭДС отдельно и током, проходящим по этой же ветви от действия каждого источника тока. При этом надо иметь в виду, что когда ведется расчет токов, вызванных каким-либо одним источником ЭДС или тока, то остальные источники ЭДС в схеме заменяются короткозамкнутыми участками, а ветви с источниками тока остальных источников отключаются (ветви с источниками тока размыкаются).

Эквивалентные преобразования схем. Во всех случаях преобразования замена одних схем другими, им эквивалентными, не должна привести к изменению токов или напряжений на участках цепи, не подвергшихся преобразованию.
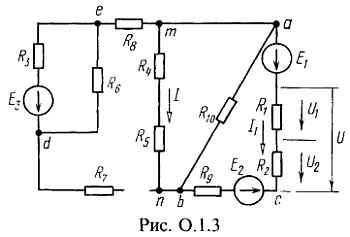
Замена последовательно соединенных сопротивлений одним эквивалентным. Сопротивления соединены последовательно, если они обтекаются одним и тем же током (например, сопротивления соединены последовательно (см. рис. 0.1,3), также последовательны сопротивления ).
Эквивалентное сопротивление цепи, состоящей из n последовательно соединенных сопротивлений, равно сумме этих сопротивлений

При последовательном соединении n сопротивлений напряжения на них распределяются прямо пропорционально этим сопротивлениям

В частном случае двух последовательно соединенных сопротивлений

где U — общее напряжение, действующее на участке цепи, содержащем два сопротивления (см. рис. 0.1.3).
Замена параллельно соединенных сопротивлений одним эквивалентным. Сопротивления соединены параллельно, если вес они присоединены к одной парс узлов, например, сопротивления (см. рис. 0.1.3).
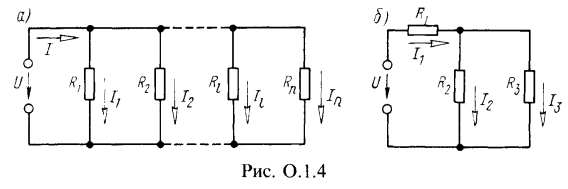
Эквивалентное сопротивление цепи, состоящей из n параллельно соединенных сопротивлений (рис. 0.1.4),

В частном случае параллельного соединения двух сопротивлений эквивалентное сопротивление

При параллельном соединении n сопротивлений (рис. 0.1.4, а) токи в них распределяются обратно пропорционально их сопротивлениям или прямо пропорционально их проводимостям

Ток в каждой из них вычисляется через ток I в неразветвленной части цепи

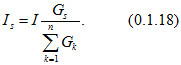
В частном случае двух параллельных ветвей (рис. 0.1.4, б)

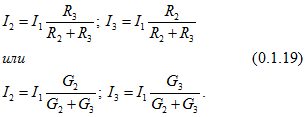
Замена смешанного соединения сопротивлений одним эквивалентным. Смешанное соединение это сочетание последовательного и параллельного соединений сопротивлений. Например, сопротивления (рис. 0.1.4, б) соединены смешанно. Их эквивалентное сопротивление

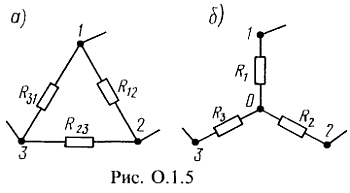
Формулы преобразования треугольника сопротивлений (рис. 0.1.5, а) в эквивалентную звезду сопротивлений (рис. 0.1.5, б), и наоборот, имеют такой вид:

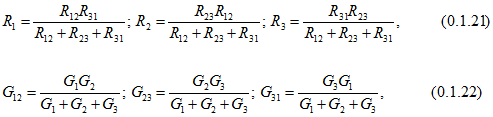
где G — проводимость соответствующей ветви.
Формулы (0.1.22) можно записать через сопротивления

Пример приведен в разделе.

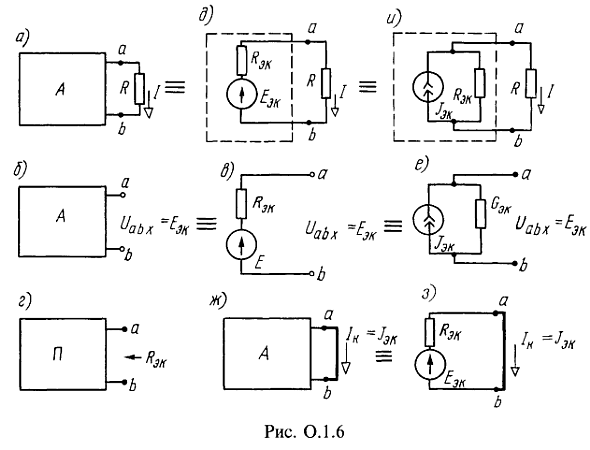
Метод эквивалентного источника (метол активного двухполюсника, или метод холостого хода и короткого замыкания). Применение метода целесообразно для определения тока в какой-либо одной ветви сложной электрической цепи. Рассмотрим два варианта: а) метод эквивалентного источника ЭДС и б) метод эквивалентного источника тока.
При методе эквивалентного источника ЭДС для нахождения тока I в произвольной ветви ab, сопротивление которой R (рис. 0.1.6, а, буква А означает активный двухполюсник), надо эту ветвь разомкнуть (рис. 0.1.6, б), а часть цепи, подключенную к этой ветви, заменить эквивалентным источником с ЭДС и внутренним сопротивлением (рис. 0.1.6, в).
ЭДС этого источника равняется напряжению на зажимах разомкнутой ветви (напряжение холостого хода):

Расчет схем в режиме холостого хода (см. рис. 0.1.6, б) для определения проводится любым известным методом.
Внутреннее сопротивление эквивалентного источника ЭДС равняется входному сопротивлению пассивной цепи относительно зажимов а и b исходной схемы, из которой исключены все источники [источники ЭДС заменены короткозамкнутыми участками, а ветви с источниками тока отключены (рис. 0.1.6, г); буква П указывает на пассивный характер цепи], при разомкнутой ветви ab. Сопротивление можно вычислить непосредственно по схеме рис. 0.1.6, г.
Ток в искомой ветви схемы (рис. 0.1.6, д), имеющей сопротивление R, определяют по закону Ома:

При методе эквивалентного источника тока для расчета тока в ветви ab, сопротивление которой R, надо заменить часть схемы относительно зажимов а и b (при разомкнутой ab) эквивалентным источником тока, ток которого , а проводимость (рис. 0.1.6, е).
Для нахождения тока надо зажимы а и b закоротить и любым способом рассчитать ток короткого замыкания , протекающий по закороченному участку (рис. 0.1.6, ж). При этом . Сопротивление можно найти, как и при расчете по методу эквивалентного источника ЭДС (см. рис. 0.1.6, г). Это же сопротивление можно рассчитать, как это видно из схемы замещения заданной схемы в режиме короткого замыкания (рис. 0.1.6, з), по формуле

Ток в ветви R (рис. 0.1.6, и)

Примеры приведены в задачах раздела.

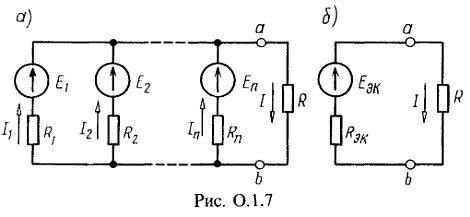
Замена нескольких соединенных параллельно источников ЭДС одним эквивалентным. Если имеется несколько источников с ЭДС и внутренними сопротивлениями , работающих параллельно на общее сопротивление нагрузки R (рис. 0.1.7, а), то они могут быть заменены одним эквивалентным источником, ЭДС которого , а внутреннее сопротивление (рис. 0.1.7, б). При этом

Токи
в сопротивлении R:
в каждой из ветвей:
где

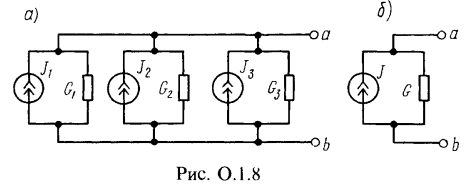
Замена паралельно соединенных источников тока одним эквивалентным. Если несколько источников тока с токами и внутренними проводимостями , соединены параллельно (рис. 0.1.8, а), то их можно заменить одним эквивалентным источником тока (рис. 0.1.8, б), ток которого равен алгебраической сумме токов, а его внутренняя проводимость равна сумме проводимостей отдельных источников