Электропроводность полупроводников
Полупроводники занимают промежуточную область между проводниками и диэлектриками. К полупроводникам относится большинство веществ, имеющихся в природе: это — минералы, различные окислы и сульфиды, металлы — кремний, германий и др. Электрическая проводимость полупроводников колеблется в широком интервале: ![]() .
.
Все электронные полупроводники являются кристаллическими веществами с различными кристаллическими решетками и электронным видом электропроводности. В узлах решетки в правильном геометрическом порядке расположены атомы элементов.
Каждый атом, находящийся в узле кристаллической решетки, имеет определенное количество электронов. В случае твердого тела огромные количества атомов заполняют малый объем, так что взаимодействие атомов вызывает расщепление энергетических уровней электронов, в результате чего образуются энергетические зоны. Точно так же как состояния электронов в изолированном атоме ограничены дискретными энергетическими уровнями, состояния электронов в твердом теле ограничены дискретными энергетическими зонами.
Зона, которая образуется из внешних валентных уровней, называется валентной или заполненной зоной. Кроме валентной зоны кристалл имеет зону проводимости, которая расположена выше валентной. Эти две зоны в диэлектриках и полупроводниках разделены запрещенной зоной, т. е. зоной, в которой не может находиться ни один электрон. Графически это изображено на рис. 5-22.
Диэлектрики, полупроводники и металлы с точки зрения зонной теории различаются только шириной запрещенной зоны. Диэлектрики имеют широкую запрещенную зону, иногда достигающую ![]() Дж (15 эВ). При температуре абсолютного нуля электронов в зоне проводимости не имеется, но при комнатной температуре в ней уже будет некоторое количество электронов, выбитых из валентной зоны за счет тепловой энергии. В проводниках (металлах) зона проводимости и валентная зона перекрываются, поэтому при температуре абсолютного нуля имеется достаточно большое количество электронов проводимости. Полупроводники имеют небольшие запрещенные зоны, и их электропроводность сильно зависит от внешних факторов.
Дж (15 эВ). При температуре абсолютного нуля электронов в зоне проводимости не имеется, но при комнатной температуре в ней уже будет некоторое количество электронов, выбитых из валентной зоны за счет тепловой энергии. В проводниках (металлах) зона проводимости и валентная зона перекрываются, поэтому при температуре абсолютного нуля имеется достаточно большое количество электронов проводимости. Полупроводники имеют небольшие запрещенные зоны, и их электропроводность сильно зависит от внешних факторов.
В идеально чистом кристалле при тем-пературе абсолютного нуля валентная зона полностью заполнена электронами, а зона проводимости пуста. При приложении электрического поля к кристаллу тока не будет. В этом случае кристалл представляет собой идеальный изолятор. При увеличении температуры часть электронов приобретает достаточную энергию, чтобы преодолеть запрещенную зону и перейти на более высокие энергетические уровни — в зону проводимости. При таком энергетическом состоянии электроны уже могут свободно двигаться в кристаллической решетке, так как они освободились от влияния ядер покинутых атомов. Эти электроны становятся достоянием всего кристалла. Под действием электрического поля электроны, имеющие энергию зоны проводимости, направленно двигаются по кристаллу, создавая электрический ток. При увеличении температуры растет число электронов в зоне проводимости, т. е. увеличивается электропроводность.
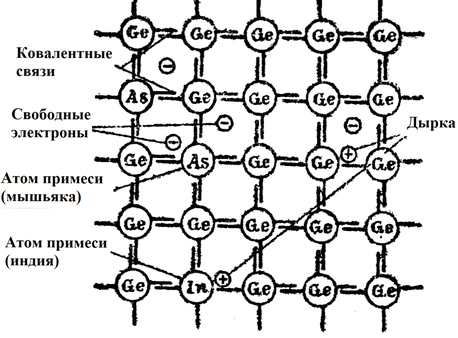
На рис. 5-23 изображена кристаллическая решетка германия не в объемном, а в плоскостном виде. В каждом узле решетки расположен атом германия, у которого на внешних валентных уровнях находятся четыре электрона. Каждый атом германия связан соответственно с четырьмя соседними атомами; эти связи условно показаны в виде двух близко расположенных друг к другу черточек. Такие связи называют двухэлектронными или ковалентными. Двухэлектронная связь является наиболее устойчивой. В идеально чистом кристалле при температуре абсолютного нуля все электроны прочно связаны с ядрами атомов и принимать участие в процессе проводимости не могут. При повышении температуры может нарушиться ковалентная связь; при этом электрон, который приобрел достаточную энергию, становится свободным, иными словами, переходит в зону проводимости. Под действием электрического поля свободный электрон будет двигаться в кристаллической решетке, создавая электрический ток. В ковалентной связи, откуда под действием теплоты был вырван электрон, осталось как бы пустое место, которое условно назвали дыркой. Дырка может быть представлена как положительный электрический заряд, равный по абсолютной величине заряду электрона. Дырка может быть занята электроном, перешедшим из соседней ковалентной связи. Ушедший электрон в свою очередь образует новую дырку. Под действием электрического поля возникает направленное перемещение электронов от дырки к дырке. Таким образом, дырки как бы перемещаются в кристаллической решетке в противоположном направлении по отношению к движению электронов. Этот процесс равносилен перемещению положительного заряда в кристалле.
Рис. 5-22. Схема энергетических зон полупроводника.
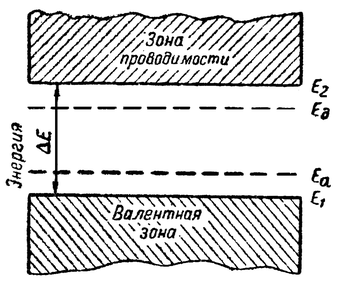
Рис. 5-23. Структура ковалентных связей и решетки четырехвалентных атомов (алмаз, германий, кремний и др.) с примесями III группы (In) и V группы (As).
![]() — наибольшее значение энергии в валентной зоне;
— наибольшее значение энергии в валентной зоне; ![]() — наименьшее значение энергии в зоне проводимости;
— наименьшее значение энергии в зоне проводимости; ![]() — ширина запрещенной зоны;
— ширина запрещенной зоны; ![]() — энергетический уровень расположения доноров;
— энергетический уровень расположения доноров; ![]() — энергетический уровень расположения акцепторов;
— энергетический уровень расположения акцепторов; ![]() — энергия ионизации донорных примесей;
— энергия ионизации донорных примесей; ![]() — энергия ионизационных акцепторных примесей.
— энергия ионизационных акцепторных примесей.
С точки зрения зонной теории дырка образуется в валентной зоне тогда, когда электрон перейдет в зону проводимости и оставит пустое место. Дырки, таким образом, перемещаются в валентной зоне и участвуют в переносе электрического заряда, увеличивая электропроводность полупроводника. Итак, в идеально чистом кристалле при определенных температурах (выше абсолютного нуля) в валентной зоне образуется определенное количество дырок, равное количеству свободных электронов в зоне проводимости. Как те, так и другие участвуют в проводимости одновременно.
Такая проводимость называется собственной и выражается уравнением
![]()
где е — заряд электрона; ![]() — подвижность электронов,
— подвижность электронов, ![]() ;
; ![]() — подвижность дырок,
— подвижность дырок, ![]() ; n — количество электронов в 1
; n — количество электронов в 1 ![]() (концентрация); р- концентрация дырок.
(концентрация); р- концентрация дырок.
Подвижность — скорость перемещения электрона (дырки) в электрическом поле с напряженностью, равной 1 В/м.
Для получения кристалла с определенным удельным сопротивлением в него вводят примеси. Если в германий введен атом пятой группы, имеющий на внешней орбите пять электронов, то четыре из них будут участвовать в ковалентных связях с атомами кристалла, а пятый окажется слабо связанным с ядром атома примеси и при небольшой температуре оторвется от ядра, становясь свободным электроном.
При введении атома третьей группы ковалентные связи не будут полностью завершены; при этом образуется дырка. На рис. 5-23 показаны атом мышьяка — пятой и атом индия — третьей групп.
Примеси, вызывающие увеличение в полупроводнике свободных электронов, получили название донорных (т. е. отдающих электроны), а примеси, вызывающие увеличение дырок, называются акцепторными (т. е. захватывающими электроны).
Зонная теория доказывает, что уровни донорных и акцепторных примесей находятся в запрещенной зоне (рис. 5-22). Проводимость, вызванная введенными примесями, называется примесной проводимостью.
Полупроводник, который имеет только донорные примеси, обладает электронной проводимостью и называется электронным (или n-типа), а имеющий только акцепторные примеси, обладает дырочной проводимостью и называется дырочным (или р-типа). Когда есть донорные и акцепторные примеси, то полупроводник обладает смешанной проводимостью.
Каждый полупроводник в определенном температурном интервале обладает за счет ионизации примесей только примесной проводимостью. С повышением температуры начинается ионизация электронов из валентной зоны в зону проводимости; при этом проявляется начало так называемой собственной проводимости. При дальнейшем увеличении температуры количество свободных электронов в зоне проводимости, перешедших из валентной зоны, становится во много раз большим, чем свободных электронов, перешедших с примесных уровней, в результате этого проявляется собственная проводимость. Температура, при которой начинается собственная проводимость, зависит от ширины запрещенной зоны данного полупроводника, количества и энергии ионизации примесей. Начало собственной проводимости характеризует верхний температурный предел работы некоторых полупроводниковых приборов.
Если в полупроводнике n-типа образуется пара электрон — дырка (например, под действием света электрон переходит из валентной зоны в зону проводимости, оставляя на своем месте дырку), то дырку называют неосновным носителем тока, а пару электрон — дырка — неравновесными носителями. В p-типе, наоборот, электрон называют неосновным носителем тока.
Для описания движения носителя тока в кристаллической решетке под действием электрического поля вводится понятие эффективной массы электрона (дырки). Носитель заряда в кристалле ведет себя подобно свободному электрону в вакууме с массой, равной эффективной массе. Она является коэффициентом пропорциональности между внешней силой (полем) и средним ускорением для носителя. В общем случае величина эффективной массы является тензором и зависит от направления поля. В практических расчетах используется скалярная величина эффективной массы, определяемая из выражения
![]()
где k — волновое число; Е — энергия.
Подвижность носителей заряда есть средняя добавочная скорость, которую они приобретают при движении в электрическом поле с напряженностью в 1 В/м, и обратно пропорциональна эффективной массе:
![]()
где ![]() — средняя статистическая скорость носителей заряда;
— средняя статистическая скорость носителей заряда; ![]() — среднее время свободного пробега
— среднее время свободного пробега
носителей заряда; Е-напряженность электрического поля.
Для практических расчетов можно использовать следующие аналитические выражения подвижностей электронов и дырок:
для германия
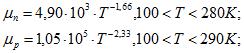
для кремния
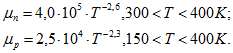
С целью определения концентрации носителей заряда в валентной зоне и зоне проводимости необходимо знать функцию распределения электронов по энергиям.
Функция распределения Ферми f(E) определяет вероятность того, что квантовое состояние с энергией Е при температуре Т занято электроном, а 1-f(E) верояность того, что состояние свободно, т. е. занято дыркой,
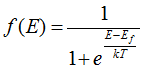
где ![]() — уровень Ферми, соответствующий значению энергии Е, для которого
— уровень Ферми, соответствующий значению энергии Е, для которого ![]() .
.
Уровень Ферми является химическим потенциалом электронного газа в расчете на один электрон.
Концентрация носителей заряда (электронов n или дырок р) в полупроводнике определяется как интеграл произведения плотности квантовых состояний N(Е) на функцию распределения Ферми f(E), взятый по всем значениям энергии в данной зоне.
Концентрация свободных электронов
![]()
Концентрация дырок
![]()
Плотность квантовых состояний
![]()
где V — объем системы; m* — эффективная масса носителя заряда.
Для невырожденного полупроводника концентрации электронов и дырок проводимости
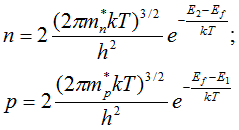
Для полупроводника с собственной проводимостью концентрации электронов ![]() и дырок
и дырок ![]() равны и определяются как
равны и определяются как
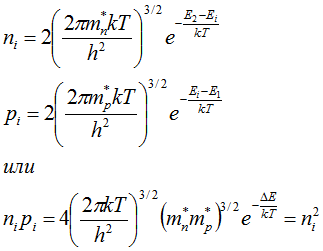
где Ei -энергия, соответствующая середине запрещенной зоны.
В собственном полупроводнике ![]() , тогда
, тогда
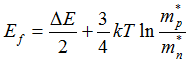
Для примесного полупроводника количество электронов на донорных уровнях равно:
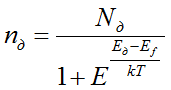
где Nд — концентрация доноров.
Количество дырок на акцепторных уровнях равно:
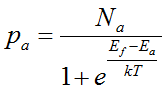
где Nа — концентрация акцепторов.
Общий случай при ![]() (слабая ионизация)
(слабая ионизация)
![]()
Концентрация электронов в зоне проводимости равна:
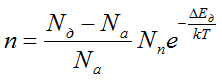
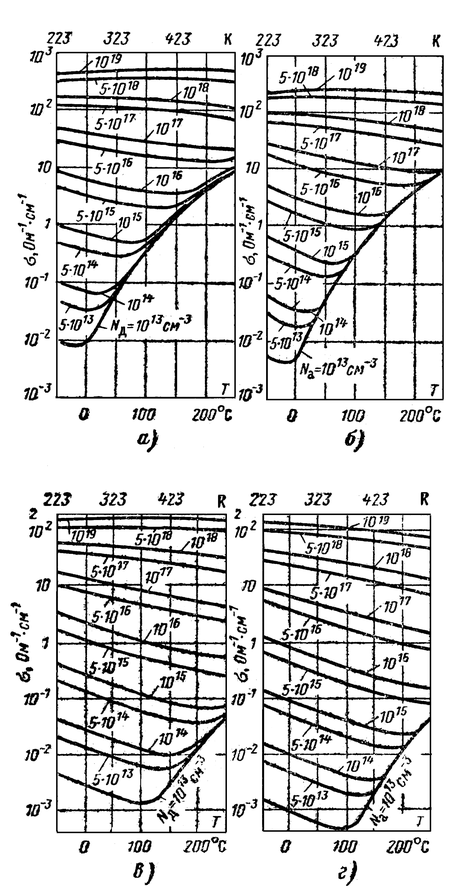
На рис, 5-24 приведены зависимости удельной электропроводности от температуры и концентрации примесей для германия и кремния.
Рис. 5-24. Зависимость удельной электрической проводимости германия и кремния. а-германий n-типа; б-германий р-типа; в-кремний n-типа; г- кремний р-типа
Электротехнические материалы
Классификация веществ по электрическим свойствам
Электропроводность диэлектриков
Электрическая прочность воздушных промежутков
Разряд по поверхности твердого диэлектрика
Электропроводность полупроводников
Получение и свойства полупроводников
Характеристики полупроводниковых материалов