Метод узловых напряжений
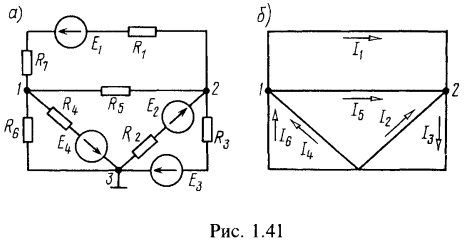
1. Для схемы рис. 1.41, а пользуясь методом узловых напряжений, определить потенциалы узловых точек 1 и 2 (потенциал точки 3 принять равным нулю). Определив потенциалы ![]() , вычислить все токи. Дано:
, вычислить все токи. Дано:![]()
Решение:
На основании (0.1.13) запишем систему уравнений для определения потенциалов точек 1 и 2: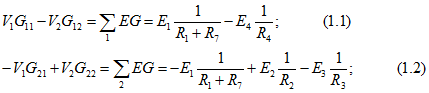
Подсчитаем ![]() —сумму проводимостей ветвей, присоединенных к узлу 1:
—сумму проводимостей ветвей, присоединенных к узлу 1:
![]()
Аналогично ![]() — сумма проводимостей ветвей, присоединенных к узлу 2:
— сумма проводимостей ветвей, присоединенных к узлу 2:
![]()
Сумма проводимостей, соединяющих первый и второй узлы,
![]()
Подставляя числовые значения в уравнения (1.1) и (1.2), получим
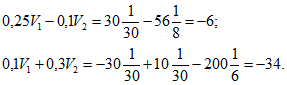
Решив последние два уравнения, найдем потенциалы точек 1 и 2: ![]() .
.
Применяя закон Ома для отдельных ветвей, определим искомые токи:
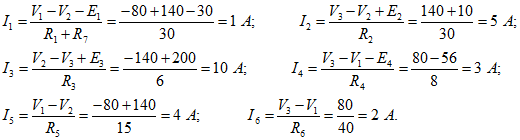
Направления найденных токов указаны на структурной схеме (рис. 1.41, б) цепи (рис. 1.41, а).
Для упражнений рекомендуем составить самостоятельно уравнения узловых напряжений в матричной форме.
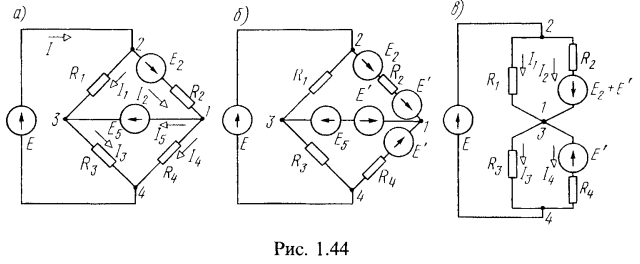
2. Методом узловых напряжений найти токи в схеме цепи (рис. 1.44,а). Дано:![]()
Решение:
Всего в схеме четыре узла ![]() , две ветви, содержащие только источники напряжения: ветви ЭДС
, две ветви, содержащие только источники напряжения: ветви ЭДС ![]() . Согласно (0.1.12 б) число уравнений, составляемых по методу узловых напряжений, равно одному:
. Согласно (0.1.12 б) число уравнений, составляемых по методу узловых напряжений, равно одному: ![]() .
.
Однако при составлении уравнений согласно формулам (0.1.13) для любого из узлов войдут слагаемые, имеющие бесконечно большую проводимость.
Покажем, как обойти указанное затруднение. Известно, что если во все ветви, примыкающие к какому-либо узлу, ввести одинаковые ЭДС, направленные к узлу (или от него), то это не окажет влияния на распределение токов в схеме, так как в уравнениях второго закона Кирхгофа для любого контура эти ЭДС взаимно компенсируются. Воспользовавшись этим свойством, введем во все ветви, примыкающие к узлу 1, ЭДС Е‘ направленные к этому узлу и равные ![]() (рис. 1.44, б). Теперь окажется, что в ветви 1—3 действуют две одинаковые и противоположно направленные ЭДС, и их сумма равна нулю. Поэтому точки 1 и 3 равнопотенциальны и их можно закоротить (рис. 1.44, в). Эта схема имеет три узла и содержит одну ветвь, имеющую только ЭДС
(рис. 1.44, б). Теперь окажется, что в ветви 1—3 действуют две одинаковые и противоположно направленные ЭДС, и их сумма равна нулю. Поэтому точки 1 и 3 равнопотенциальны и их можно закоротить (рис. 1.44, в). Эта схема имеет три узла и содержит одну ветвь, имеющую только ЭДС ![]() . Поэтому согласно (0.1.12 б) по методу узловых напряжений надо составить всего одно уравнение. Составим его для базисного узла 1, приняв
. Поэтому согласно (0.1.12 б) по методу узловых напряжений надо составить всего одно уравнение. Составим его для базисного узла 1, приняв ![]() . Тогда
. Тогда ![]() . Уравнение для узла 1 имеет такой вид:
. Уравнение для узла 1 имеет такой вид:

Подставляя сюда числовые значения, получим ![]() .
.
Найдем токи в ветвях исходной схемы по закону Ома: ![]()
Токи в ветвях с ЭДС ![]() определим по первому закону Кирхгофа:
определим по первому закону Кирхгофа:
![]()
Для упражнения рекомендуется решить эту задачу, введя в каждую из ветвей, примыкающую к узлу 2, ЭДС Е» = Е.