Трансформаторные подстанции высочайшего качества

При изменении тока в одном из индуктивно связанных элементов цепи (см. рис. 6.1 и 6.2) в другом элементе возникает ЭДС взаимной индукции и между его разомкнутыми выводами появляется напряжение. Абсолютные значения ЭДС и напряжений, обусловленных взаимной индукцией (закон электромагнитной индукции),

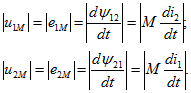
Для облегчения решения вопроса о знаке этих величин прибегают к специальной разметке выводов индуктивно связанных элементов цепи.
Два вывода, принадлежащих двум разным индуктивно связанным элементам цепи, называют одноименными и обозначают одинаковыми значками, руководствуясь следующим правилом: при одинаковом направлении токов относительно одноименных выводов магнитные потоки самоиндукции и взаимной индукции в каждом элементе должны суммироваться.
Применим это правило для разметки выводов катушек, показанных на рис. 6.3, а. При направлении тока от вывода а к выводу b и тока от вывода с к выводу d магнитные потоки самоиндукции (или ) и взаимной индукции суммируются. Поэтому вывод а одноименен с выводом с и аналогично вывод b одноименен с выводом d. Для катушек, показанных на рис. 6.3,б, одноименными являются выводы и , а также и . Разница с предыдущим случаем обусловлена другим направлением намотки витков второй катушки.
Одну из двух пар одноименных выводов обозначают специальными значками, например точками, звездочками, треугольниками и т. п.

Рис. 6.3

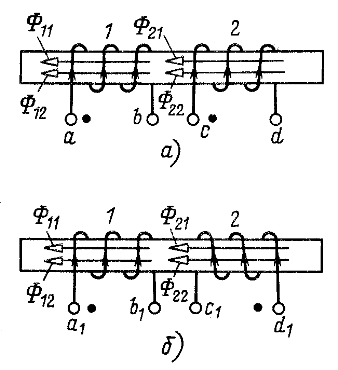
Рис. 6.4

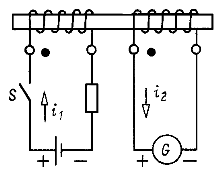
Рис. 6.5

Установить взаимное расположение катушек и направление намотки их витков так просто, как на рис. 6.3, не всегда представляется возможным. Но найти одноименные выводы можно на основании простого опыта, для которого требуются гальванический элемент (или аккумулятор) и гальванометр. Одна из катушек соединяется с гальванометром, другая подключается к гальваническому элементу (рис. 6.4). При замыкании ключа S кратковременно возникает ток , ослабляющий магнитное поле, созданное током . Следовательно, в момент включения источника питания токи , и направлены относительно одноименных выводов противоположно. Направление тока определяется полярностью источника питания. О направлении тока судят по кратковременному отклонению стрелки гальванометра. Если стрелка отклоняется в сторону шкалы (имеется в виду гальванометр с односторонней шкалой), то ток направлен к положительному выводу гальванометра (рис. 6.4), при этом выводы катушек, присоединенные к положительным выводам гальванометра и источника питания, одноименны, точно так же одноименны и выводы катушек, присоединенные к отрицательным выводам гальванометра и источника питания; заметим, что в момент отключения источника питания стрелка гальванометра вновь отклоняется, но уже в обратном направлении, так как ток противодействует уменьшению магнитного поля.
Перейдем теперь к решению вопроса о знаке в выражениях для ЭДС и напряжения, обусловленных взаимной индукцией.

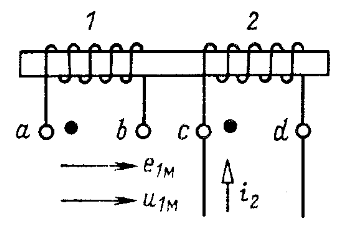
Рассмотрим две катушки (рис. 6.5). Пусть катушка 1 разомкнута, а в катушке 2 протекает синусоидальный ток . Выберем положительные направления для ЭДС и напряжения в катушке 1 и для тока в катушке 2 относительно одноименных выводов одинаковыми, например от а к b и соответственно от с и d.
Прежде всего отметим, что при одинаковых положительных направлениях напряжения и ЭДС их значения численно равны, но противоположны по знаку: . Действительно, когда , потенциал вывода b больше потенциала вывода а, и, следовательно, .
Электродвижущая сила на основании закона Ленца должна иметь такое направление, при котором вызываемый ею ток препятствовал бы изменению магнитного потока взаимной индукции. Поэтому, если , то ЭДС должна иметь действительное направление от b к а, т. е. . Если , то ЭДС должна иметь действительное направление от а к b, т. е. .
Таким образом, при выбранных положительных направлениях (рис. 6.5) знаки и всегда противоположны, поэтому



Для комплексных величин получим

Если бы положительные направления для и в катушке 1 и тока в катушке 2 относительно одноименных выводов были выбраны различными, то аналогичные рассуждения показали бы, что знаки и всегда были бы одинаковы: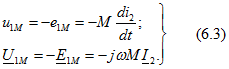



Из (6.2) и (6.3) видно, что напряжение , обусловленное взаимной индукцией, сдвинуто по фазе относительно тока на угол или . Знак этого угла зависит от выбора положительных направлений и относительно одноименных выводов.
Величина имеет размерность сопротивления, называется сопротивлением взаимной индукции и обозначается . Величина называется комплексным сопротивлением взаимной индукции и обозначается . Таким образом,

Рис. 6.6

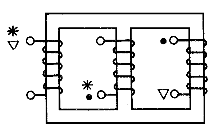
Если индуктивно связаны между собой не два, а несколько элементов цепи, надо у каждого из них отметить выводы, одноименные с выводами остальных элементов, при этом в общем случае приходится прибегать к разным условным обозначениям. Поясним это на примере трех катушек, расположенных, как указано на рис. 6.6.
Верхний вывод первой катушки одноименен с нижними выводами второй и третьей катушек, но эти последние не являются одноименными по отношению друг к другу, поэтому их нельзя обозначить одинаковыми значками. На рис. 6.6 одноименные выводы первой и второй катушек обозначены звездочками, первой и третьей — треугольниками, а второй и третьей — точками. В частных случаях для разметки одноименных выводов нескольких катушек можно обойтись одним условным обозначением. Убедиться в этом можно на примере нескольких катушек, расположенных вдоль одной оси (аналогично рис. 6.3).
При большом числе индуктивно связанных элементов цепи указанная выше система разметки одноименных выводов получается недостаточно наглядной, так как приходится вводить много различных обозначений. В таких случаях удобнее другая система разметки, при которой взаимные индуктивности считают алгебраическими величинами.
Сначала совершенно произвольно указывают направления обхода каждого индуктивно связанного элемента цепи, например ставят букву н у вывода, от которого начинается обход, и букву к у другого вывода. Затем указывают знаки взаимных индуктивностей, руководствуясь следующим правилом. Если при совпадении направлений токов с выбранными направлениями обходов потоки взаимной индукции и потоки самоиндукции суммируются, то соответствующая взаимная индуктивность положительна, если же они вычитаются, то соответствующая взаимная индуктивность отрицательна.
Примем, например, для катушек, показанных на рис. 6.6, за начала обхода верхние выводы и за концы обхода — нижние выводы, при этом взаимные индуктивности будут отрицательны .
Знаки в выражениях для напряжений, обусловленных взаимной индуктивностью, получаются, конечно, такими же, как и при первой системе разметки выводов; при совпадении положительных направлений и с принятыми направлениями обходов получаем , при несовпадении получаем , при этом взаимная индуктивность считается величиной алгебраической и берется с тем знаком, который для нее указан при разметке выводов.
Вторая система разметки при наличии только двух индуктивно связанных элементов менее удобна, так как требует не только маркировки выводов, но и указания знака взаимной индуктивности. В дальнейшем применяется только первая система разметки.