Трансформаторные подстанции высочайшего качества

Для анализа и расчетов несимметричных режимов в трехфазных цепях широко применяется метод симметричных составляющих. Он основан на представлении любой трехфазной несимметричной системы величин (токов, напряжений, магнитных потоков) в виде суммы в общем случае трех симметричных систем величин. Эти симметричные системы, которые в совокупности образуют несимметричную систему величин, называются ее симметричными составляющими. Симметричные составляющие отличаются друг от друга порядком следования фаз, т. е. порядком, в котором фазные величины проходят через максимум, и называются системами прямой, обратной и нулевой последовательностей.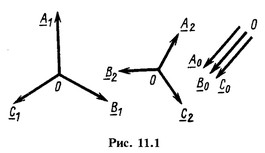
Обозначим трехфазную систему величин (токов, напряжений, магнитных потоков) для общности буквами А, В и С. Величины, относящиеся к системам прямой, обратной и нулевой последовательностей, отметим соответственно индексами 1, 2 и 0. На рис. 11.1 показан пример векторных диаграмм симметричных составляющих всех трех последовательностей.
Система прямой последовательности имеет порядок следования фаз А, В, С. Система обратной последовательности имеет порядок следования фаз А, С, В. Система нулевой последовательности состоит из трех одинаковых величин, совпадающих по фазе. Для этих трех систем можно записать

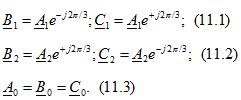
Комплексное число называется фазным множителем и сокращенно обозначается буквой а:

Умножение вектора на а соответствует повороту его против направления движения часовой стрелки (вперед) на 120° или повороту по направлению движения часовой стрелки (назад) на 240°:

Умножение вектора на соответствует повороту его вперед на 240° или повороту назад на 120°.
При помощи фазного множителя выражения (11.1) и (11.2) можно записать так:

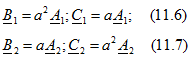
Кроме того,

Пользуясь соотношением (11.8), можно исключать из формул множитель а в степени выше второй:

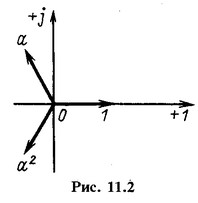
Как следует из (11.4) и (11.5), 1, образуют симметричную систему единичных векторов (рис. 11.2). Их сумма

Докажем теперь, что любую несимметричную систему векторов можно разложить на симметричные системы прямой, обратной и нулевой последовательностей. Если это имеет место, то

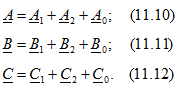
Выразим в этих предполагаемых равенствах все векторы симметричных систем через векторы , пользуясь соотношениями (11.3), (11.6) и (11.7):

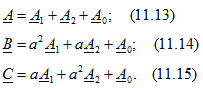
Получены три уравнения, из которых однозначно можно определить векторы , что и доказывает возможность разложения заданной несимметричной системы векторов на три симметричные системы.
После сложения уравнений (11.13) — (11.15) получим

откуда с учетом (11.9) найдем, что

Умножая (11.14) на а и (11.15) на и затем складывая уравнения (11.13) — (11.15), находим, что

Умножая (14.14) на и (11.15) на а и затем складывая уравнения (11.13) — (11.15), получаем