Законы Кирхгофа в матричной форме
Для записи законов Кирхгофа в матричной форме необходимо составить топологические матрицы схемы.
Матрица соединений, или узловая А,- это таблица коэффициентов независимых уравнений, составленных по первому закону Кирхгофа для У — 1 узлов. Строки (i) соответствуют узлам (их число равно У- 1), столбцы (j) — ветвям (их число равно В). Элемент матрицы aij = + 1, если ветвь j графа соединена с узлом i и направлена от узла i (положительное направление тока в ветви j выбрано от узла i). Элемент матрицы aij = — 1, если ветвь j графа соединена с узлом i и направлена к узлу i. Элемент матрицы aij = 0, если ветвь j не присоединена к узлу i.
Например, для схемы и графа по рис. 1.14 с У= 4 узлами и В = 6 ветвями для первых трех узлов

что соответствует первым трем уравнениям ( 1.21а).
Так как -матрица А определяет, какие ветви присоединены к каждому узлу и как направлены токи в этих ветвях, то произведение матрицы соединений на матрицу-столбец токов ветвей I дает совокупность левых частей уравнений, составленных по первому закону Кирхгофа, и, следовательно, равно нулю:
АI = 0 (1.26а)
— это первый закон Кирхгофа в матричной форме. Для схемы и графа по рис. 1.14
![]()
и после выполнения умножения матриц получаем первые три уравнения (1.21а).
Под матрицей соединений иногда понимают матрицу А, записанную для всех узлов схемы.
Матрица сечений Q — это таблица коэффициентов, составленных по первому закону Кирхгофа для сечений. Строки i матрицы соответствуют сечениям (их число равно У — 1), столбцы j — ветвям (их число равно В). Элемент матрицы qij = +1, если ветвь j содержится в сечении i и направлена согласно с направлением сечения. Элемент матрицы qij = -1, если ветвь j содержится в сечении i и направлена противоположно направлению сечения. Элемент матрицы qij = 0, если ветвь j не содержится в сечении i. Для главных сечений составляется матрица главных сечений.
Например, для графа рис. 1.14, д при показанных трех главных сечениях
В матричной форме первый закон Кирхгофа можно записать и с матрицей сечений
QI=0 (1.26 б)
После умножения матрицы Q на матрицу-столбец токов I получаются первое и третье (с обратным знаком) уравнения (1.21а) и уравнение (1.216), т. е. независимая система уравнений по первому закону Кирхгофа.
Матрица контуров В — это таблица коэффициентов независимых уравнений, составленных по второму закону Кирхгофа для К = В — (У- 1) независимых контуров. Строки к соответствуют контурам (их число равно К), столбцы j — ветвям (их число равно В).
Элемент матрицы bkj=+1, если ветвь j входит в состав контура k и ее направление совпадает с направлением обхода контура. Элемент матрицы bkj,= -1, если ветвь j входит в состав контура k и ее направление противоположно направлению обхода контура. Элемент матрицы bkj = 0, если ветвь j не входит в состав контура k.
Матрица В, составленная для главных контуров, приводит непосредственно к независимой системе уравнений по второму закону Кирхгофа. Например, для графа рис. 1.14, д с контурами, состоящими из ветвей 2-4-3 (а), 5-6-4 (б) и 1-6-3 (в) матрица главных контуров при их обходе по направлению движения часовой стрелки

Умножив матрицу В на матрицу-столбец напряжений ветвей, получим матричное уравнение по второму закону Кирхгофа в формулировке (1.20а)
BU = 0, (1.27)
так как каждая строка матрицы В определяет, какие ветви входят в соответствующий контур и с какими знаками должны быть записаны напряжения ветвей.
Для схемы по рис. 1.14, а и ее графа по рис. 1.14, в после умножения на матрицу-столбец напряжений ветвей
![]()
получим систему трех независимых уравнений вида (1.20а):
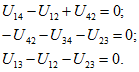
Эта система с учетом равенства ![]() и соотношений (1.22а) совпадает с ранее полученной системой (1.23), (1.246), (1.24а), т. е. с системой вида (1.206).
и соотношений (1.22а) совпадает с ранее полученной системой (1.23), (1.246), (1.24а), т. е. с системой вида (1.206).
Для любой планарной схемы, т. е. схемы, которую можно изобразить на листе без пересекающихся ветвей и проводов, в качестве независимых контуров можно выбирать элементарные контуры-ячейки. Например, для схемы рис. 1.14, а это ячейки I, II, III. Если выбрать направление обхода каждой ячейки по направлению движения стрелки часов, то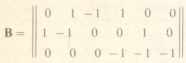
После умножения на матрицу-столбец напряжений ветвей U получим другую независимую систему уравнений по второму закону Кирхгофа в форме (1.20 а):
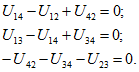
которая после подстановки соотношений (1.22а) приводится к виду (1.206).
Если схема цепи кроме источников ЭДС, как на рис. 1.14, а (и далее рис. 1.20-1.22), содержит и источники тока, то для записи матричных уравнений (1.27) можно рекомендовать преобразование источников тока в источники ЭДС (см. рис. 1.23) или введение понятия обобщенной ветви (см. рис. 1.25).
Электрические цепи постоянного тока
Пример расчета цепей постоянного тока
Элементы электрических цепей и схем
Схемы замещения источников энергии
Закон Ома для участка цепи с ЭДС
Баланс мощностей для простой неразветвленной цепи
Законы Кирхгофа и их применение
Топологические графы
Законы Кирхгофа в матричной форме
Метод узловых потенциалов
Метод контурных токов
Уравнения цепи в матричной форме
Расширенные узловые уравнения
Преобразования в линейных электрических схемах
Принцип наложения (суперпозиции)
Свойство взаимности
Входные и взаимные проводимости, коэффициенты передачи
Принцип компенсации. Зависимые источники
Общие замечания о двухполюсниках и многополюсниках
Линейные соотношения между напряжениями и токами
Теорема о взаимных приращениях токов и напряжений
Принцип эквивалентного генератора
Передача энергии от активного двухполюсника к пассивному