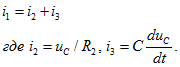Расчет переходных процессов в цепях первого порядка
1. При замыкании контакта ![]() и разомкнутом контакте
и разомкнутом контакте ![]() к источнику постоянного напряжения подключается индуктивная катушка
к источнику постоянного напряжения подключается индуктивная катушка ![]() , последовательно с которой соединен реостат сопротивлением
, последовательно с которой соединен реостат сопротивлением ![]() (рис. 8.4, а). Через
(рис. 8.4, а). Через ![]() после замыкания
после замыкания ![]() замыкается
замыкается ![]() , который остается в таком состоянии продолжительное время.
, который остается в таком состоянии продолжительное время.
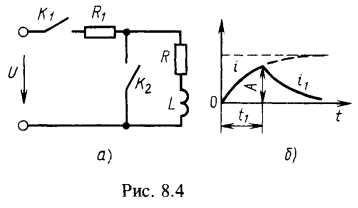
Построить кривую изменения тока в катушке с момента замыкания контакта ![]() до момента практически полного затухания тока в катушке (например, до 1% от максимального значения тока).
до момента практически полного затухания тока в катушке (например, до 1% от максимального значения тока).
Решение:
При замыкании ![]() и разомкнутом
и разомкнутом ![]() переходный ток в катушке
переходный ток в катушке
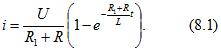
К моменту включения ![]() ток в катушке
ток в катушке
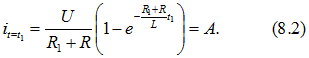
Второй закон Кирхгофа для контура катушки, замкнутой контактом ![]() (при
(при ![]() ), будет
), будет
![]()
Решение этого уравнения дает
![]()
Постоянную интегрирования А найдем из начального условия, согласно которому для момента ![]() ток
ток ![]() . Ток, по формуле (8.3):
. Ток, по формуле (8.3):
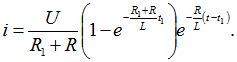
На рис. 8.4, б построены кривые изменения тока.
2. Для замедления скорости нарастания тока в электромагните ![]() его шунтируют резистивным сопротивлением
его шунтируют резистивным сопротивлением ![]() (рис. 8.8, а). Найти ток i в электромагните и сравнить скорость его нарастания со скоростью нарастания тока электромагнита при отсутствии шунта. Для упрощения положить
(рис. 8.8, а). Найти ток i в электромагните и сравнить скорость его нарастания со скоростью нарастания тока электромагнита при отсутствии шунта. Для упрощения положить ![]() .
.
Решение:
Ток в катушке ищем в виде суммы установившегося и свободного токов
![]()
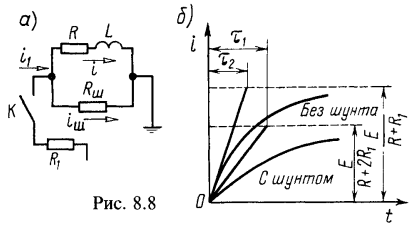
Установившийся ток — это постоянный ток, который рассчитываем по методу расчета цепей постоянного тока:
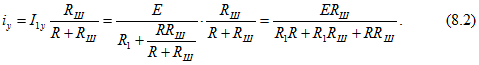
Свободный ток
![]()
где р — корень следующего характеристического уравнения
![]()
отсюда находим
![]()
Постоянная времени цепи
![]()
Подставляем (8.2) и (8.3) в (8.1):
![]()
Для определения постоянной А используем начальное условие, согласно которому при t=0 ток ![]() :
:
![]()
отсюда
![]()
Подставляя это выражение в (8.6), получим искомый ток
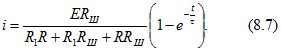
В частном случае при ![]() ток
ток
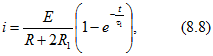
где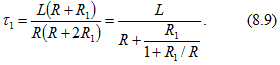
Бхли же шунт снять, то, полагая в (8.7) ![]() , получим
, получим
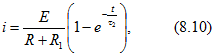
где![]()
Сравнивая выражения (8.9) и (8.11), устанавливаем, что ![]() , т. е. постоянная времени при наличии шунта больше, чем без него.
, т. е. постоянная времени при наличии шунта больше, чем без него.
Вычислим начальную скорость нарастания тока. При наличии шунта из формулы (8.8) имеем
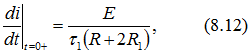
а без шунта из формулы (8.10) получим
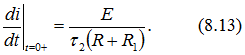
Сравнивая выражения (8.12) и (8.13), устанавливаем, что при наличии шунта скорость нарастания тока меньше, чем без него. На рис. 8.8, б по уравнениям (8.8) и (8.10) построены кривые токов.
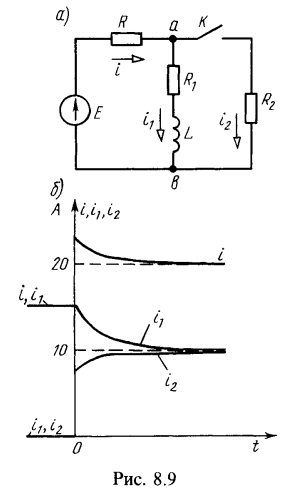
3. В цепи (рис. 8.9, а) дано: ![]() . Найти токи после внезапного замыкания контакта (до коммутации в цепи был установившийся режим). Построить кривые изменения этих величин.
. Найти токи после внезапного замыкания контакта (до коммутации в цепи был установившийся режим). Построить кривые изменения этих величин.
Решение:
Расчет токов в докоммутационном режиме (контакт разомкнут): ![]()
![]()
Расчет установившегося режима после коммутации (контакт замкнут):
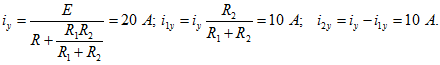
Расчет переходного режима. Решение целесообразно начать с отыскания тока ![]() в ветви с индуктивным элементом, так как при этом наиболее просто воспользоваться начальным условием. Ток ищем в виде
в ветви с индуктивным элементом, так как при этом наиболее просто воспользоваться начальным условием. Ток ищем в виде ![]() .
.
Свободная составляющая этого тока ![]() , где
, где ![]() — корень характеристического уравнения, которое наиболее просто составить относительно ветви с индуктивностью:
— корень характеристического уравнения, которое наиболее просто составить относительно ветви с индуктивностью:![]()
Отсюда ![]()
Подставляя в выражение ![]() найденные значения установившегося
найденные значения установившегося ![]() и свободного
и свободного ![]() токов, будем иметь
токов, будем иметь ![]()
Постоянную А определяем из начального условия ![]() или 10+А=15, отсюда А = 5.
или 10+А=15, отсюда А = 5.
Итак,
![]()
Для отыскания тока ![]() вначале найдем напряжение на параллельном участке:
вначале найдем напряжение на параллельном участке:![]()
Наконец, вычисляем искомые токи:
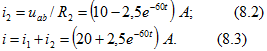
Отметим, что в ветвях с ![]() в момент коммутации имеет место скачкообразное изменение токов; это возможно, так как в этих ветвях нет накопителей энергии и поэтому оно не связано с внезапным изменением в них запаса электромагнитной энергии и становится физически осуществимым.
в момент коммутации имеет место скачкообразное изменение токов; это возможно, так как в этих ветвях нет накопителей энергии и поэтому оно не связано с внезапным изменением в них запаса электромагнитной энергии и становится физически осуществимым.
На рис. 8.9, б построены кривые токов в докоммутационном и послекоммутационном режимах.
4. Найти ток в индуктивной катушке (рис. 8.10, а) после включения источника постоянного тока J (т. е. при размыкании контакта К).
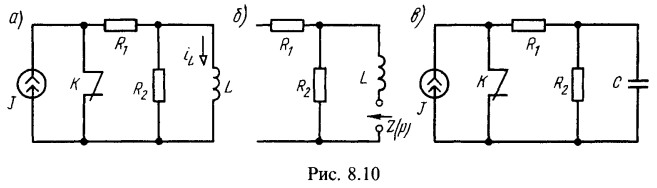
Решение:
Искомый ток ![]() ищем в виде суммы установившегося и свободного токов
ищем в виде суммы установившегося и свободного токов
![]()
Из схемы очевидно, что при установившемся режиме ток
![]()
Для определения вида свободного тока составляем выражение характеристического сопротивления относительно ветви с индуктивностью (рис. 8.10, б, при этом согласно п. 3 основных положений и соотношений ветвь с источником тока должна быть разомкнута), которое приравниваем нулю: ![]() , отсюда
, отсюда ![]() .
.
Таким образом, свободный ток ищем в виде
![]()
Подставляем (8.2) и (8.3) в (8.1), получим
![]()
Постоянную интегрирования А находим из начального условия
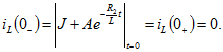
Отсюда находим A=-J, подставляем в (8.4) и окончательно получим 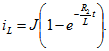
Обращаем внимание на то, что ![]() в решение не вошло, так как оно соединено последовательно с источником тока, сопротивление которого бесконечно велико.
в решение не вошло, так как оно соединено последовательно с источником тока, сопротивление которого бесконечно велико.
5. Цепь (рис. 8.18, а), параметры которой ![]()
![]()
![]()
![]()
![]() при разомкнутом контакте К находится в установившемся режиме под воздействием постоянной ЭДС Е=15 В.
при разомкнутом контакте К находится в установившемся режиме под воздействием постоянной ЭДС Е=15 В.
После включения требуется определить: 1) начальные значения переходных токов и напряжения на конденсаторе, а также начальные значения их установившихся и свободных составляющих и производную свободной составляющей напряжения на конденсаторе в момент начала переходного процесса; 2) законы изменения во времени всех токов и напряжения на конденсаторе.
Решение:
Расчет режима до коммутации (контакт разомкнут). Токи в ветвях и напряжение на конденсаторе равны:![]()
Расчет установившегося режима после коммутации (контакт замкнут). Напряжение на конденсаторе и токи:![]()
Определение законов изменения во времени искомых величин.
Расчет свободного процесса. Составим для послекоммутационной схемы характеристическое уравнение сопротивления и приравняем его нулю. Наиболее просто составить его относительно ветви с конденсатором:![]()
Корень этого уравнения
![]()
Так как характеристическое сопротивление имеет только один корень, свободная составляющая каждого искомого значения имеет вид ![]() .
.
Расчет переходного процесса:![]()
Постоянную А определяем из начального условия: ![]() или 12,5=10+А, откуда -А = 2,5.
или 12,5=10+А, откуда -А = 2,5.
Таким образом, ![]() . Находим токи
. Находим токи
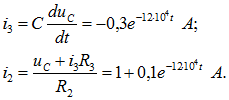
Расчеты занесены в табл. 1 (даны округленные значения). Графики найденных значений изображены на рис. 8.18, б.
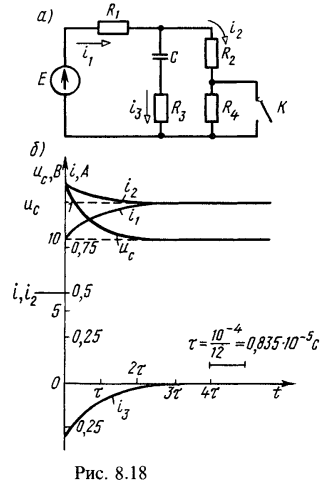
Таблица 1
| 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| 12,5 | 12,22 | 11,97 | 11,74 | 11,54 | 11,37 | 11,22 |
| 1,1 | 1,089 | 1,079 | 1,070 | 1,062 | 1,055 | 1,049 |
| -0,3 | -0,266 | -0,236 | -0,209 | -0,186 | -0,165 | -0,146 |
6. В схеме рис. 8.22 до замыкания контакта К был установившийся режим. Дано: ![]()
![]()
![]() . Найти напряжение на конденсаторе и ток в неразветвленной части цепи после замыкания контакта.
. Найти напряжение на конденсаторе и ток в неразветвленной части цепи после замыкания контакта.
Решение:
Вначале вычислим сопротивление конденсатора, необходимое для дальнейших расчетов:
![]()
Расчет режима до коммутации. Сначала найдем комплексные амплитуды тока ![]() и напряжения на конденсаторе
и напряжения на конденсаторе ![]()
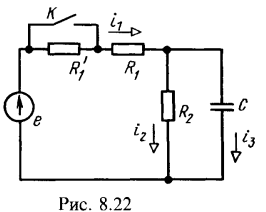
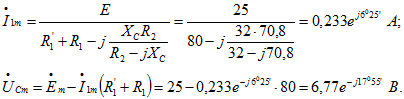
Соответствующие мгновенные значения:![]()
Расчет комплексных амплитуд тока и напряжения на конденсаторе в установившемся режиме после коммутации
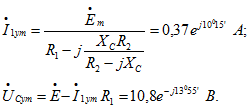
Соответствующие мгновенные значения:![]()
Расчет свободного процесса. Для послекоммутациониой схемы наиболее просто составить характеристическое сопротивление относительно ветви с емкостью. Для нахождения корня приравниваем сопротивление нулю: ![]() , отсюда
, отсюда
![]()
Свободное напряжение на конденсаторе ищем в виде ![]() .
.
Расчет переходного процесса после коммутации. Напряжение на конденсаторе находим в виде ![]() . Постоянную интегрирования А находим из начального условия, согласно второму закону коммутации:
. Постоянную интегрирования А находим из начального условия, согласно второму закону коммутации: ![]() , или
, или ![]() , отсюда А=0,5.
, отсюда А=0,5.
Итак, напряжение на конденсаторе ![]()
Находим ток в неразветвленной части цепи