Расчет цепей с зависимыми источниками
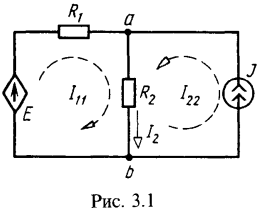
1. В цепи (рис. 3.1) действуют независимый источник тока J и ИНУТ (источник напряжения, управляемый током) с ЭДС ![]() . Дано:
. Дано: ![]() . Найти напряжение
. Найти напряжение ![]() .
.
Решение:
Выберем для решения метод контурных токов.
Контурное уравнение: ![]() .
.
Учитывая, что ![]() , получим
, получим ![]() .
.
Из этого уравнения определим ток ![]() . Напряжение
. Напряжение ![]() .
.
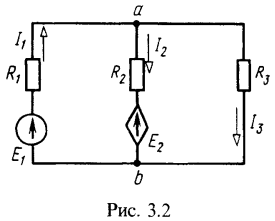
2. В цепи (рис. 3.2) действуют независимый источник напряжения с ЭДС ![]() и ИНУН (источник напряжения, управляемый напряжением) с ЭДС
и ИНУН (источник напряжения, управляемый напряжением) с ЭДС ![]() . Найти токи в ветвях, если
. Найти токи в ветвях, если ![]() .
.
Решение:
Для решения выберем метод узловых напряжений. Приняв ![]() , запишем уравнение для узла а
, запишем уравнение для узла а
![]()
Учитывая, что ![]() , имеем
, имеем
![]()
Решая уравнение, получим ![]() . Токи в ветвях:
. Токи в ветвях:
![]()
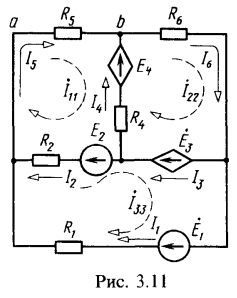
3. Для цепи (рис. 3.11), содержащей зависимые источники ![]() , найти все токи. Дано:
, найти все токи. Дано:![]()
Решение:
Решим задачу методом контурных токов.
Контурные токи: ![]() токи в ветвях:
токи в ветвях:![]() Зависимые источники выражаются так:
Зависимые источники выражаются так: ![]() Уравнения контурных токов:
Уравнения контурных токов:
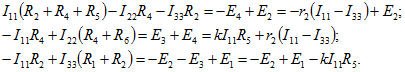
Группируя неизвестные и подставляя числовые данные, получим:
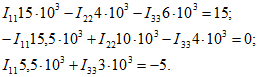
Решение системы уравнений определяет контурные токи: ![]() Токи в ветвях равны:
Токи в ветвях равны:
![]()
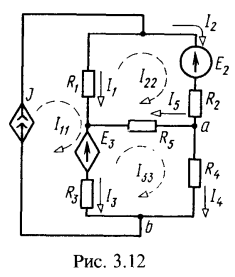
4. В цепи (рис. 3.12). содержащей ИТУН (источник тока, управляемый напряжением) ![]() и ИНУТ
и ИНУТ ![]() , найти токи в ветвях методом контурных токов. Дано:
, найти токи в ветвях методом контурных токов. Дано:![]()
Решение:
Направления контурных токов и токов ветвей указаны на рис. 3.12. Токи ветвей: ![]() . Зависимые источники выражаются:
. Зависимые источники выражаются: ![]() .
.
Уравнения контурных токов:
![]()
Подставляя полученные выражения для ![]() , имеем
, имеем
![]()
Подстановка числовых данных и решение уравнений определяют контурные токи: ![]() токи в ветвях
токи в ветвях ![]() .
.
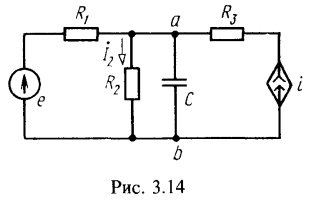
5. В цепи (рис. 3.14), содержащей ИТУТ (источник тока, управляемый током), действует источник напряжения ![]() . Найти напряжение
. Найти напряжение ![]() , если
, если ![]() . Комплексный ток зависимого источника
. Комплексный ток зависимого источника ![]() .
.
Решение:
Комплексное действующее значение напряжения источника ЭДС ![]() . Так как цепь содержит
. Так как цепь содержит
два узла, решим задачу методом узловых напряжений. При ![]() уравнение для узла а имеет вид
уравнение для узла а имеет вид
![]()
Комплексный ток ![]() . Тогда
. Тогда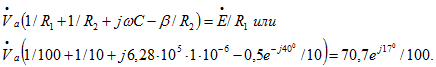
Отсюда находим ![]() .
.