Расчет переходных процессов в цепях с взаимной индуктивностью
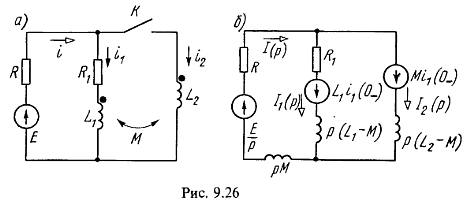
1. До замыкания контакта К цепь рис. 9.26, а находилась в установившемся режиме. Найти выражение тока 
как функцию времени после замыкания. Дано: 
. Составить операторную схему замещения.
Решение:
Для схемы после коммутации запишем уравнения Кирхгофа для мгновенных значений:
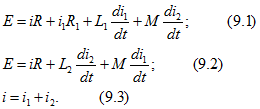
Перейдем к операторной форме записи этих уравнений, учтя ненулевое значение тока 
:
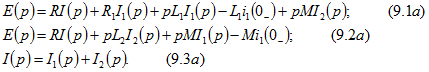
Решим эти уравнения относительно 
, и, учитывая, что 
, найдем
Подставив числовые значения и сократив числитель и знаменатель на общий множитель р+ 1000, получим
Проверка. При 
ток 
, что соответствует первому закону коммутации. При 
ток 
. Действительно, при установившемся режиме ветвь 
будет закорочена индуктивностью, по которой проходит ток 
. Схема замещения изображена на рис. 9.26. б.
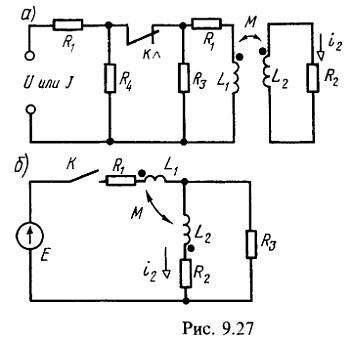
2. Схемы рис. 9.27, а и б имеют индуктивно-связанные элементы. Для каждой из них найти ток 
после коммутации.
В схеме рис. 9.27, а до размыкания контакта К имел место установившийся режим, вызванный действием постоянных источников. Для этой схемы рассмотреть случаи, когда к входным зажимам был подведен: 1) источник постоянного напряжения U=100 В; 2) источник постоянного тока J=0,5 А. Параметры этой схемы:
Параметры схемы на рис. 9.27, б:
Решение:
1) Для схемы рис. 9.27, а как при действии U, так и J
2) Для схемы рис. 9.27, б
