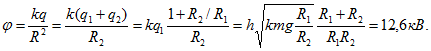Решение задач по определению потенциала, работы электрических сил
1 Найти потенциал шара радиуса R = 0,1 м, если на расстоянии r=10м от его поверхности потенциал электрического поля 
Решение:
Поле вне шара совпадает с полем точечного заряда, равною заряду q шара и помещенного в его центре. Поэтому потенциал в точке, находящейся на расстоянии R + r от центра шара, φr= kq/(R + r); отсюда q = (R + r)φr/k. Потенциал на поверхности шара
2 N одинаковых шарообразных капелек ртути одноименно заряжены до одного и того же потенциала φ. Каков будет потенциал Ф большой капли ртути, получившейся в результате слияния этих капель?
Решение:
Пусть заряд и радиус каждой капельки ртути равны q и r. Тогда ее потенциал φ = kq/r. Заряд большой капли Q = Nq, и если ее радиус равен R, то ее потенциал Ф = kQ/R = kNq/R = Nφr/R. Объемы маленькой и большой капель 
и 
связаны между собой соотношением V=Nυ. Следовательно, 
и потенциал
3 В центре металлической сферы радиуса R = 1 м, несущей положительный заряд Q=10нКл, находится маленький шарик с положительным или отрицательным зарядом |q| = 20 нКл. Найти потенциал φ электрического поля в точке, находящейся на расстоянии r=10R от центра сферы.
Решение:
В результате электростатической индукции на внешней и внутренней поверхностях сферы появятся равные по модулю, но противоположные по знаку заряды (см. задачу 25 и рис. 332). Вне сферы потенциалы электрических полей, создаваемых этими зарядами, в любой точке равны по модулю и противоположны по знаку. Поэтому потенциал суммарного поля индуцированных зарядов равен нулю. Таким образом, остаются лишь поля, создаваемые вне сферы зарядом BQ на ее поверхности и зарядом шарика q. Потенциал первого поля в точке удаленной от центра сферы на расстояние r, 
, а потенциал второго поля в той же точке 
. Полный потенциал 
. При q=+20нКл φ=27В; при q=-20нКл φ=-9В.
4 До какого потенциала можно зарядить находящийся в воздухе (диэлектрическая проницаемость ε=1) металлический шар радиуса R = 3 см, если напряженность электрического поля, при которой происходит пробой в воздухе, Е=3 МВ/м?
Решение:
Наибольшую напряженность электрическое поле имеет у поверхности шара:
Потенциал шара 
; отсюда φ=ER=90 В.
5 Два одинаково заряженных шарика, расположенных друг от друга на расстоянии r = 25 см, взаимодействуют с силой F=1 мкН. До какого потенциала заряжены шарики, если их диаметры D = 1 см?
Решение:
Из закона Кулона определяем заряды шариков: 
. Заряд q, находящийся на шарике радиуса R = D/2, создает на поверхности этого шарика потенциал
В том месте, где находится этот шарик, заряд другого шарика создает потенциал 
. Таким образом, потенциал каждого шарика
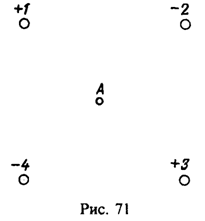
6 В вершинах квадрата расположены точечные заряды (в нКл): q1 = +1, q2 = -2, q3= +3, q4 = -4 (рис. 71). Найти потенциал и напряженность электрического поля в центре квадрата (в точке А). Диагональ квадрата 2а = 20 см.
Решение: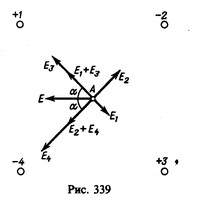
Потенциал в центре квадрата равен алгебраической сумме потенциалов, создаваемых всеми зарядами в этой точке:
Напряженность поля в центре квадрата является векторной суммой напряженностей, создаваемых каждым зарядом в этой точке:
Модули этих напряженностей
Удобно сначала сложить попарно векторы, направленные по одной диагонали в противоположные стороны (рис. 339): E1 + E3 и E2 + E4. При данных зарядах сумма E1 + E3 по модулю равна сумме Е2 + Е4. Поэтому результирующая напряженность Е направлена по биссектрисе угла между диагоналями и составляет с этими диагоналями углы α=45°. Ее модуль E=2545 В/м.
7 Найти потенциалы и напряженности электрического поля в точках а и b, находящихся от точечного заряда q=167нКл на расстояниях rа = 5 см и rb = 20 см, а также работу электрических сил при перемещении точечного заряда qo = 1 нКл из точки а в точку b.
Решение:
Напряженности электрического поля в точках а и b
Потенциалы в этих точках
Работа электрических сил при перемещении заряда q0 из точки а в точку b
8 Точечный положительный заряд q создает в точках а и b (рис. 72) поля с напряженностями Еa и Еb. Найти работу электрических сил при перемещении точечного заряда qo из точки а в точку b.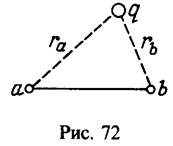
Решение:
Напряженности электрического поля в точках а и b равны
где 
—расстояния точек а и b от заряда q. Потенциалы в точках а и b равны
отсюда работа, необходимая для перемещения заряда qo из точки а в точку b,
9 В атомной физике энергию быстрых заряженных частиц выражают в электрон-вольтах. Электрон-вольт (эВ) — это такая энергия, которую приобретает электрон, пролетев в электрическом поле путь между точками, разность потенциалов между которыми равна 1 В. Выразить электрон-вольт в джоулях. Какую скорость имеет электрон, обладающий энергией 1 эВ?
Решение:
При прохождении электроном разности потенциалов V= 1 В электрические силы совершают над электроном работу
Эта работа равна кинетической энергии, приобретенной электроном, т.е.
Поскольку
10 Электрон летит от точки а к точке b, разность потенциалов между которыми V= 100 В. Какую скорость приобретает электрон в точке b, если в точке а его скорость была равна нулю?
Решение:
Работа электрических сил равна изменению кинетической энергии электрона:
11 Какую работу необходимо совершить при переносе точечного заряда qo=30 нКл из бесконечности в точку, находящуюся на расстоянии r=10 см от поверхности заряженного металлического шара? Потенциал на поверхности шара φ = 200 В, радиус шара R = 2 см.
Решение:
Потенциал на поверхности шара φ = kq/R; отсюда его заряд q = φR/k. Потенциал на расстоянии R + r от центра шара 
При переносе заряда qo из точки с потенциалом 
в бесконечность работа электрических сил 
мкДж. Такую же работу необходимо совершить против электрических сил при переносе заряда qo из бесконечности в точку, находящуюся на расстоянии r от поверхности шара.
12 При переносе точечного заряда qo=10 нКл из бесконечности в точку, находящуюся на расстоянии r=20 см от поверхности заряженного металлического шара, необходимо совершить работу А =0,5 мкДж. Радиус шара R=4 см. Найти потенциал φ на поверхности шара.
Решение:
13 Два одинаковых заряда qo=q=50 мкКл находятся на расстоянии ra=1 м друг от друга. Какую работу А надо совершить, чтобы сблизить их до расстояния rb=0,5 м?
Решение:
14 Два заряда qa=2 мкКл и qb=5 мкКл расположены на расстоянии r=40 см друг от друга в точках а и b (рис. 73). Вдоль прямой cd, проходящей параллельно прямой ab на расстоянии d=30см от нее, перемещается заряд qo=100мкКл. Найти работу электрических сил при перемещении заряда qo из точки с в точку d, если прямые ас и bd перпендикулярны к прямой cd.
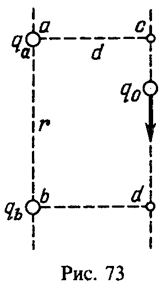
Решение:
15 Два параллельных тонких кольца радиуса R расположены на расстоянии d друг от друга на одной оси. Найти работу электрических сил при перемещении заряда qo из центра первого кольца в центр второго, если на первом кольце равномерно распределен заряд q1, а на втором — заряд q2.
Решение: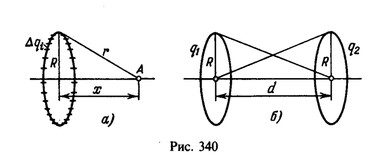
Найдем потенциал, создаваемый зарядом q, находящимся на кольце, в точке А на оси кольца, расположенной на расстоянии
х от его центра (рис. 340, а) и, следовательно, на расстояниях 
от точек, лежащих на кольце. Разобьем кольцо на отрезки, малые по сравнению с расстоянием r. Тогда заряд 
, находящийся на каждом отрезке (i — номер отрезка), можно рассматривать как точечный. Он создает в точке А потенциал 
. Потенциал, создаваемый в точке А всеми отрезками кольца (отстоящими от этой точки на одно и то же расстояние r), будет
В скобках стоит сумма зарядов всех отрезков, т. е. заряд всего кольца q; поэтому
Потенциал Ф1 поля в центре первого кольца складывается из потенциала, создаваемого зарядом q1, находящимся на первом кольце, для которого х=0, и потенциала, создаваемого зарядом q2, находящимся на втором кольце, для которого x=d (рис. 340, б). Аналогично находится потенциал в центре второго кольца:
Окончательно для работы имеем
16 На тонком кольце радиуса R равномерно распределен заряд q. Какова наименьшая скорость υ, которую необходимо сообщить находящемуся в центре кольца шарику массы т с зарядом qo, чтобы он мог удалиться от кольца в бесконечность?
Решение:
Если заряды qo и q одного знака, то удалить шарик от кольца в бесконечность можно, сообщив ему бесконечно малую скорость. Если же знаки зарядов разные, то сумма кинетической и потенциальной энергий шарика в центре кольца должна быть равна нулю, так как она равна нулю в бесконечности: 
, где φ=kq/R — потенциал в центре кольца (см. задачу 17); отсюда
17 На шарик радиуса R=2 см помещен заряд q=4 пКл. С какой скоростью подлетает к шарику электрон, начавший движение из бесконечно удаленной от него точки?
Решение:
18 Между горизонтально расположенными пластинами плоского конденсатора с высоты Н свободно падает незаряженный металлический шарик массы т. На какую высоту h после абсолютно упругого удара о нижнюю пластину поднимется шарик, если в момент удара на него переходит заряд q? Разность потенциалов между пластинами конденсатора равна V, расстояние между пластинами равно d.
Решение:
Внутри конденсатора имеется однородное электрическое поле с напряженностью Е= V/d, направленной вертикально. После удара шарик приобретает заряд того же знака, что и нижняя пластина конденсатора. Поэтому на него будет действовать со стороны электрического поля сила F=qE=qV/d, направленная вверх. Согласно закону сохранения энергии изменение энергии равно работе внешних сил (в данном случае — электрических). Учитывая, что удар абсолютно упругий и что в начальный и конечный моменты шарик имеет лишь потенциальную энергию в поле силы тяжести, получим
откуда
19 Два шарика с одинаковыми зарядами q расположены на одной вертикали на расстоянии Н друг от друга. Нижний шарик закреплен неподвижно, а верхний, имеющий массу m, получает начальную скорость v, направленную вниз. На какое минимальное расстояние h приблизится верхний шарик к нижнему?
Решение:
Согласно закону сохранения энергии
где qV—работа электрических сил, V=kq/H—kq/h — разность потенциалов точек начального и конечного положения верхнего шарика. Для определения h получаем квадратное уравнение: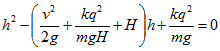
Решая его, найдем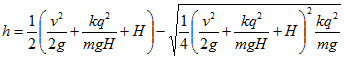
(знак плюс перед корнем соответствовал бы максимальной высоте, достигнутой шариком, если бы он получил ту же начальную скорость, направленную вверх).
20 Найти максимальное расстояние h между шариками в условиях предыдущей задачи, если неподвижный шарик имеет отрицательный заряд q, а начальная скорость v верхнего шарика направлена вверх.
Решение: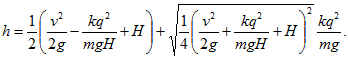
21 Электрон, пролетая в электрическом поле путь от точки а к точке b, увеличил свою скорость с νa=1000 км/с до νab = 3000 км/с. Найти разность потенциалов между точками а и b электрического поля.
Решение:
Работа, совершенная над электроном электрическим полем, идет на увеличение кинетической энергии электрона:
откуда
где γ— удельный заряд электрона. Разность потенциалов отрицательна. Так как электрон имеет отрицательный заряд, то скорость электрона увеличивается при его движении в сторону возрастания потенциала.
22 В плоский конденсатор влетает электрон со скоростью ν = 20 000 000 м/с, направленной параллельно пластинам конденсатора. На какое расстояние h от своего первоначального направления сместится электрон за время пролета конденсатора? Расстояние между пластинами d=2 см, длина конденсатора l=5 см, разность потенциалов между пластинами v=200 В.
Решение:
За время пролета t = l/v электрон смещается в направлении действия силы на расстояние
где γ — удельный заряд электрона.
23 Положительно заряженная пылинка массы 
г находится в равновесии внутри плоского конденсатора, пластины которого расположены горизонтально. Между пластинами создана разность потенциалов V1=6000 В. Расстояние между пластинами d=5см. На какую величину необходимо изменить разность потенциалов, чтобы пылинка осталась в равновесии, если ее заряд уменьшился на qo=1000 e?
Решение:
На пылинку действуют сила тяжести mg и сила 
со стороны электрического поля, где 
—начальный заряд пылинки и E1 = V1/d—напряженность электрического поля в конденсаторе.
Чтобы пылинка могла находиться в равновесии, верхняя пластина конденсатора должна быть заряжена отрицательно. При равновесии
mg = F, или 
; отсюда 
.
Так как уменьшение заряда пылинки на qo=1000e равносильно увеличению положительного заряда на qo, то новый заряд пылинки q2 = q1+qo. При равновесии 
, где V2—новая разность потенциалов между пластинами. Учитывая выражения для q2, q1 и q0, найдем
Таким образом, разность потенциалов нужно изменить на V2— V1 = — 980 В (знак минус показывает, что ее нужно уменьшить, так как заряд пылинки увеличился).
24 Решить предыдущую задачу, считая пылинку заряженной отрицательно.
Решение:
Верхняя пластина конденсатора должна быть заряжена положительно. Новый заряд пылинки q2 = q1-qo, где qo=1000e.
Поэтому (см. задачу 23)
Напряжение между пластинами нужно увеличить на V2— V1 = 1460 В.
25 В электрическое поле плоского конденсатора, пластины которого расположены горизонтально, помещена капелька масла, имеющая заряд q=1 е. Напряженность электрического поля подобрана так, что капелька покоится. Разность потенциалов между пластинами конденсатора V =500 В, расстояние между пластинами d=0,5 см. Плотность масла 
. Найти радиус капельки масла.
Решение:
При равновесии
откуда 
26 Внутри плоского конденсатора, пластины которого расположены вертикально, помещена диэлектрическая палочка длины l=1 см с металлическими шариками на концах, несущими заряды +q и — q(|q|=1 нКл). Палочка может вращаться без трения вокруг вертикальной оси, проходящей через ее середину. Разность потенциалов между пластинами конденсатора V=3 В, расстояние между пластинами d=10см. Какую работу необходимо совершить, чтобы повернуть палочку вокруг оси на 180° по отношению к тому положению, которое она занимает на рис. 74?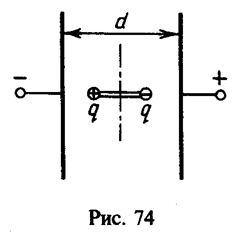
Решение:
Напряженность электрического поля в конденсаторе E=V/d.
Разность потенциалов между точками, где расположены заряды,
где 
—потенциал в точке расположения заряда + q, а 
—потенциал в точке расположения заряда — q; при этом 
. При повороте палочки электрические силы совершают работу по переносу заряда — q из точки а в точку b и заряда + q из точки b в точку а, равную
Знак минус означает, что работу должны совершить внешние силы.
27 Внутри плоского конденсатора помещен диэлектрический стержень длины l=3 см, на концах которого имеются два точечных заряда + q и —q (|q|=8нКл). Разность потенциалов между пластинами конденсатора V=3 В, расстояние между пластинами d=8 см. Стержень ориентирован параллельно пластинам. Найти момент сил, действующий на стержень с зарядами.
Решение:
28 На концах диэлектрической палочки длины l=0,5 см прикреплены два маленьких шарика, несущих заряды — q и +q (|q|=10 нКл). Палочка находится между пластинами конденсатора, расстояние между которыми d=10cм (рис.75). При какой минимальной разности потенциалов между пластинами конденсатора V палочка разорвется, если она выдерживает максимальную силу растяжения F=0,01 Н? Силой тяжести пренебречь.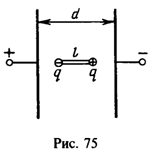
Решение: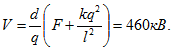
29 Металлический шарик 1 радиуса R1=1 см прикреплен с помощью диэлектрической палочки к коромыслу весов, после чего весы уравновешены гирями (рис. 76). Под шариком 1 помещают заряженный шарик 2 радиуса R2=2 см. Расстояние между шариками h = 20 см. Шарики 1 и 2 замыкают между собой проволочкой, а потом проволочку убирают. После этого оказывается, что для восстановления равновесия надо снять с чашки весов гирю массы m = 4мг. До какого потенциала j был заряжен шарик 2 до замыкания его проволочкой с шариком 1?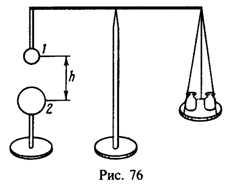
Решение:
Если до замыкания шарик 2 имел заряд 0, то сумма зарядов шариков 1 и 2 после замыкания q1+q2 = q. Потенциалы же их после замыкания одинаковы: 
. Следовательно, 
После замыкания шарик 2 действует на шарик 1 с силой
откуда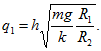 
Начальный потенциал шарика 2