Аналитический метод разложения периодических кривых в ряд Фурье
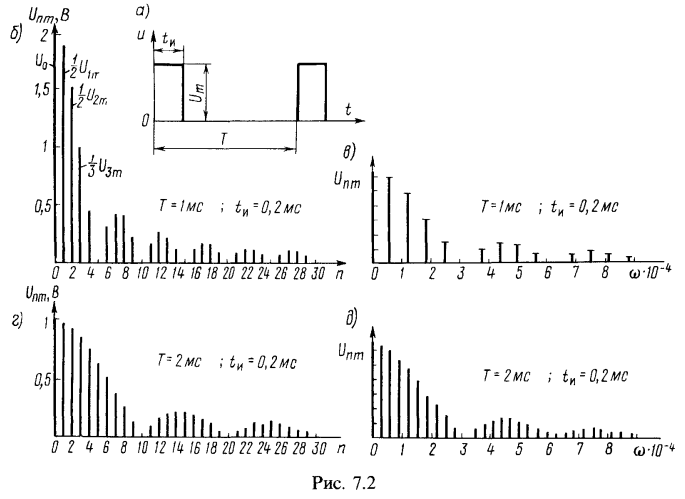
1. Разложить в тригонометрический ряд функцию, выражаемую кривой периодических импульсов напряжения постоянной амплитуды 
длительностью 
(рис. 7.2, а). Дано: 
.
Полученную функцию представить также в виде комплексного ряда Фурье. Построить амплитудно-частотный спектр в зависимости от: а) номера гармоники n и б) угловой частоты ω. Такие же спектры построить, если Т=2 мс, остальные данные те же.
Решение:
Уравнение заданной кривой: в интервале от t=0 до 
, в интервале от 
до 
.
Разбивая область интегрирования на два участка, учитывая, что 
, находим коэффициенты ряда и начальные фазы гармоник:
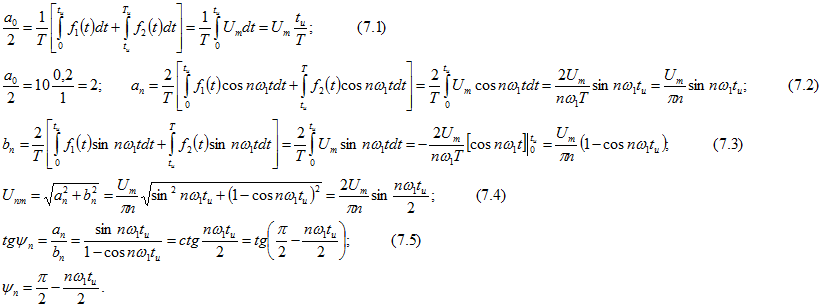
Вычисляем коэффициенты ряда и начальные фазы гармоник. При этом имеем в виду, что
Для удобства расчеты сведены в таблицу 1.
| Таблица 1 | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| n | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
 | 0 |  |  |  |  |  |  |  |  |  |  |
 | 0 | 0,2π | 0,4π | 0,6π | 0,8π | π | 1,2π | 1,4π | 1,6π | 1,8π | 2π |
 | 0 | 0,588 | 0,951 | 0,951 | 0,588 | 0 | -0,588 | -0,951 | -0,951 | -0,588 | 0 |
 | 2 | 3,74 | 3,03 | 2,02 | 0,935 | 0 | -0,624 | -0,866 | -0,757 | -0,416 | 0 |
 | - | 0,3π | 0,1π | -0,1π | -0,3π | - | -0,7π | -0,9π | -1,1π | -1,3π | - |
Искомый ряд
или, учитывая, что 
, окончательно получим
Для определения ряда Фурье в комплексной форме находим комплексные амплитуды
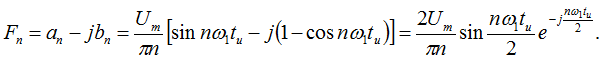
Таким образом, комплексная форма ряда Фурье
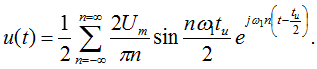
На основе полученных результатов на рис. 7.2, б изображен амплитудно-частотный спектр напряжения в зависимости от номера гармоники (расчеты для n от 1 до 10 даны в таблице 1; аналогичные расчеты для n=11…30 рекомендуется проделать самостоятельно).
По данным таблицы 1 на рис. 7.2, в построен амплитудно-частотный спектр в зависимости от 
. Для построения графика выбраны масштабы: по оси абсцисс одному делению соответствует 
; по оси ординат в одном делении 
(при построении последнего графика спектральные амплитуды приведены к нормированному масштабу путем деления на 
).
На рис. 7.2, г построен амплитудно-частотный спектр в зависимости от n при Т=2 мс, а на рис. 7.2, д спектр изображен в нормированном масштабе в зависимости от 
(расчеты рекомендуется проделать самостоятельно).
Из рис. 7.2, в и д видно, что спектральные характеристики импульсов одной и той же длительности 
зависят от периода Т следования импульсов, и чем он больше, тем гуще располагаются спектральные линии, а амплитуды соседних гармоник близки по значению.
На рис. 7.2, б-д отложены значения 
, соответствующие положительным частотам. Полный спектр можно получить, если построить такой же график симметрично относительно вертикальной оси (т. е. отложить соответствующие отрезки для отрицательных частот).