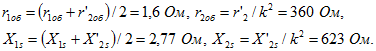Трансформаторные подстанции высочайшего качества

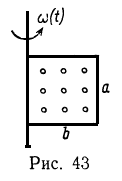
1. Прямоугольная рамка размером aXb метров вращается вокруг стороны а в однородном магнитном поле В с переменной угловой скоростью . Определить величину индуцированной ЭДС , если в начальный момент рамка перпендикулярна к полю.

Решение. Найдем закон движения Рамки (т. е. зависимость ), если в начальный момент угол между перпендикуляром к плоскости рамки и полем равен (рис. 43):

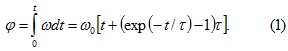
Магнитный поток через плоскость рамки запишем в виде

По определению ЭДС индукции равна

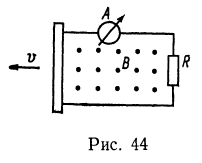
2. Два параллельных провода, замкнутых на одном конце сопротивлением R, расположены в однородном магнитном поле с индукцией В. Считая, что поле В перпендикулярно плоскости проводов, найдите ток I, который течет через проводящую перекладину между проводами, двигающуюся с постоянной скоростью (рис. 44). Расстояние между проводами равно .

Решение. На электроны в перекладине действует сила Лоренца

С силой (1) связано электрическое поле

которое появляется в системе координат, связанной с перекладиной. Это поле приводит к ЭДС индукции

Поэтому через перекладину потечет ток

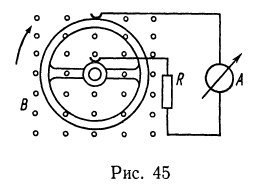
3. Медный диск радиуса а=10 см вращается в однородном магнитном поле, делая N=100 оборотов в секунду. Магнитное поле направлено перпендикулярно плоскости диска и имеет индукцию . Две щетки, одна на оси диска, другая на окружности (рис. 45), соединяют диск с внешней цепью, в которую включены реостат с сопротивлением R=10 Ом и амперметр, сопротивлением которого можно пренебречь.
Что показывает амперметр?

Решение. В системе координат, связанной с диском, возникает электрическое поле

которое приводит к ЭДС индукции

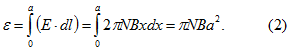
Ток по закону Ома

4. В середине длинного соленоида на расстоянии b=5 см от его оси расположен электрон. В момент времени t=0 через соленоид начинают пропускать ток, изменяющийся со временем по закону . Найдите мгновенное ускорение электрона, считая поле внутри соленоида однородным. , число витков на единицу длины соленоида витков/м, начальная скорость электрона равна нулю.

Решение. Магнитное поле внутри соленоида равно

Переменное магнитное поле приводит к вихревому электрическому полю

Мгновенное ускорение

5. Найдите коэффициент самоиндукции L длинного соленоида. Число витков на единицу длины равно n, а длина соленоида .

Решение. Магнитное поле внутри соленоида можно найти по теореме Стокса

где I — ток в обмотке соленоида. Магнитный поток через все витки, если пренебречь рассеянным полем, равен

где S — площадь поперечного сечения соленоида.
С другой стороны, известно следующее выражение для магнитного потока:

Используя (1) — (3), окончательно находим

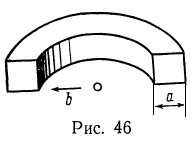
6. Тороидальная катушка из N витков, внутранний радиус которой равен b, в поперечном сечении имеет форму квадрата со стороной а (рис. 46). Найдите индуктивность катушки L.

Решение. Магнитное поле внутри катушки можно найти по теореме Стокса

где I — ток, протекающий по обмотке катушки и .
Энергия магнитного поля внутри катушки

С другой стороны, магнитная энергия катушки равна

Сравнивая (2) и (3), находим для самоиндукции катушки

7. На тороидальную катушку намотаны две вплотную прилегающие друг к другу системы обмоток с полными числами витков . Считая радиус одного витка обмотки равным r и радиус тора — R (r<<R), найдите коэффициент взаимной индукции катушек.

Решение. Магнитное поле, создаваемое одной катушкой внутри тора, равно



где — ток в обмотке первой катушки. Магнитный поток через все витки второй катушки



где S — площадь поперечного сечения тора.
Так как, с другой стороны, известно, что



то используя (1)—(3), окончательно находим для коэффициента взаимоиндукции

8. Катушка, индуктивность которой L=10 мГн и сопротивление R=2 Ом, подключается к источнику постоянного напряжения U=50 В. Чему равно время релаксации для этой катушки? С какой скоростью нарастает ток в начальный момент? Чему равно установившееся значение тока?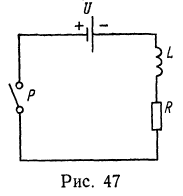

Решение. По условию в момент t=0 включает рубильник Р (рис. 47). По 2-му закону Кирхгофа имеем

решая (1), находим

где время релаксации

Скорость нарастания тока в начальный момент

Установившееся значение тока

9. Найдите действующее и среднее значение тока, график изменения которого за период Т показан на рис. 48.

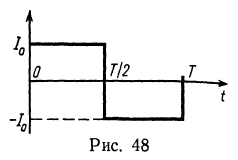Решение. По определению действующее значение

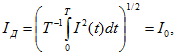
среднее значение

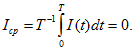
10. Катушка с индуктивностью L=50 мГн и активным сопротивлением r=10 Ом подключена к источнику синусоидального напряжения, действующее значение которого , а частота v=50 Гц. Определить полное сопротивление катушки, ток и сдвиг фаз между напряжением и током.

Решение. По определению:

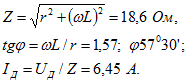
11. В схеме, показанной на рис. 49, рассчитать токи через сопротивления . Емкость С=3,18 мкФ, ЭДС генератора , а частота v=50 кГц. Как сдвинут по фазе ток через сопротивление относительно тока через .

Решение. Составляем уравнения для контурных токов, считая начальную фазу ЭДС равной нулю:

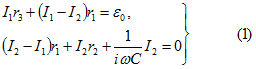
или

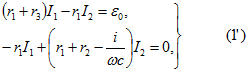
Решая систему (1′), находим:

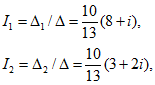
где

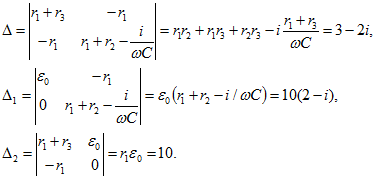
Физический ток через сопротивление равен контур, ному току , т. е.

Физический ток через сопротивление равен контурному току , т. е.

Физический ток через сопротивление равен разности контурных токов , т. е.

Ток через сопротивление сдвинут по фазе относительно тока через на угол

12. Найдите, пользуясь векторным методом, напряжение на конденсаторе в схеме на рис. 50, если параметры схемы таковы, что напряжение отстает по фазе от напряжения генератора на угол .

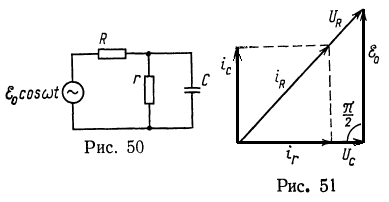Решение. Векторная диаграмма имеет вид, изображенный на рис. 51. Используя закон Ома и теорему Пифагора, получаем уравнение

откуда

13. Определить емкость С, которую надо включать последовательно с катушкой, имеющей активное сопротивление r=10 Ом и индуктивность 3,18 мГн для того, чтобы цепь была настроена в резонанс при частоте . Найти напряжение на конденсаторе при резонансе, добротность и затухание контура и полосу пропускания, если к контуру приложено напряжение U=100 В.

Решение. По определению резонансная частота

откуда

Добротность контура

Напряжение на конденсаторе при резонансе

Затухание контура

Полоса пропускания контура

14. Найти резонансную частоту и полное сопротивление параллельного контура, изображенного на рис. 52, при резонансе. Параметры контура равны: . Рассчитать добротность контура и токи, проходящие через каждую из ветвей контура, и в неразветвленной части при резонансе, если к контуру приложено напряжение U=200 В.

Решение. Рассчитаем прежде всего добротность контура

Так как добротность велика, то резонансную можно найти по приближенной формуле

Сопротивление контура при резонансе

Ток в неразветвленной части цепи при резонансе

Ток в левой ветви контура при резонансе

Ток в правой ветви контура при резонансе

15. Когда катушка со стальным сердечником (дросселем) включена на напряжение , по ней проходит ток , отстающий по фазе от напряжения на угол , причем . Эта же катушка без стального сердечника при том же напряжении потребляет ток , отстающий от напряжения на угол , причем . Определить потери мощности в стали и проводах катушки.

Решение. В катушке без сердечника имеются потери мощности только в проводах катушки:

Учитывая, что , находим активное сопротивление проводов катушки r:

Катушка со стальным сердечником потребляет мощность

причем потери в проводах равны

а потери в стальном сердечнике

16. Опыты с однофазным повышающим трансформатором дали следующие результаты напряжения, тока и мощности в первичной обмотке:
а) в режиме холостого хода (хх)

б) в режиме короткого замыкания (кз)

Предполагая, что активное и реактивное сопротивления рассеяния первичной обмотки равны соответственным приведенным сопротивлениям вторичной обмотки, т. е. определить их величины, если коэффициент трансформации . При холостом ходе можно пренебречь падением напряжения в первичной обмотке, а при коротком замыкание — намагничивающей составляющей первичного тока.

Решение. Эквивалентная схема трансформатора изображена на рис. 53.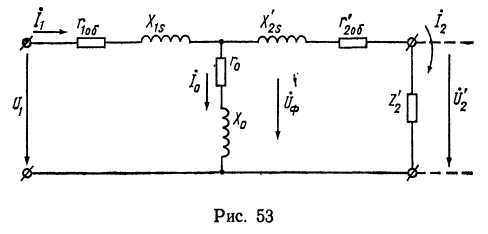

Из опыта холостого хода, пренебрегая ряжения в первичной обмотке, имеем

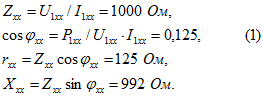
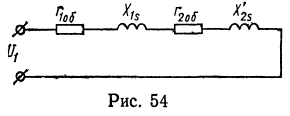В случае режима короткого замыкания, если пренебречь намагничивающей составляющей первичного тока, эквивалентная схема трансформатора имеет вид, изображенный на рис. 54. Поэтому для опыта короткого замыкания

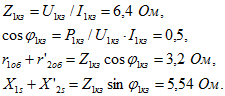
Воспользовавшись равенствами

окончательно получим