Трансформаторные подстанции высочайшего качества

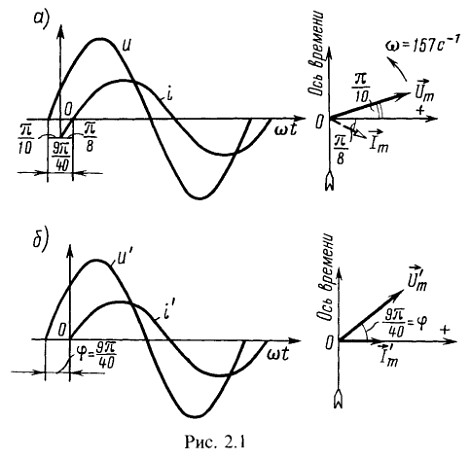
1. Построить кривые изменения напряжения и тока во времени и начертить векторы, изображающие заданные синусоидальные функции:

Чему равен сдвиг фаз между напряжением и током? Определить период, частоту, моменты начала положительных полуволн напряжения и тока. Какой вид примут уравнения для заданных напряжения и тока, если фазу, равную нулю, принять для тока? Для этого случая построить синусоиды напряжения и тока, векторную диаграмму.

Решение:
Синусоиды u и i и соответствующие им векторы изображены на рис. 2.1, а.
Период ,
частота .
Ток по фазе отстает от напряжения на угол

Моменты начала положительной полуволны напряжения и тока

При начальной фазе тока, равной нулю, уравнения
для напряжения и тока примут такой вид:

Кривые u‘, i‘ и соотвегствующие им векторы изображены на рис. 2.1, б.

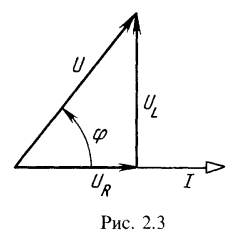
2. Катушка с резистивным сопротивлением R=10 Ом, индуктивностью L=0,05 Гн подключена к источнику синусоидального напряжения, действующее значение которого U=120B, а частота f= 50 Гц. Определить полное сопротивление катушки, ток и сдвиг фаз между напряжением и током. Чему равны активная, реактивная и полная мощности?
Вычислить активную и реактивную составляющие напряжения на зажимах катушки. Чему равна ЭДС самоиндукции, наводимая в катушке? Построить векторную диаграмму напряжений и тока.

Решение:

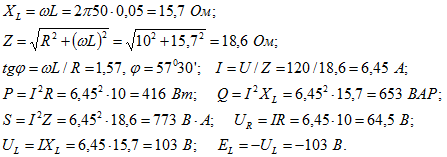
Векторная диаграмма приведена на рис. 2.3

3. К последовательно соединенным реостату сопротивлением R=120 Ом и конденсатору емкостью С=30 мкФ подведено напряжение u=311sin314t, В.
Вычислить полное сопротивление цепи, действующие значения напряжений и тока, мощность, расходуемую в цени, реактивную мощность и разность фаз напряжения и тока. Построить векторную диаграмму напряжений и тока.

Решение:

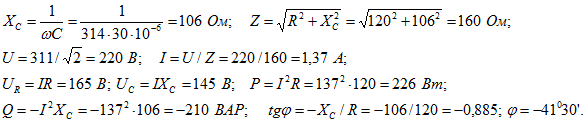
Векторная диаграмма приведена на рис. 2.6.

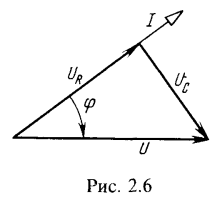
4. Последовательно с реостатом, имеющим сопротивление , включена катушка, параметры которой (рис. 2.7, а). Определить ток в цени, разность фаз между напряжением и током, напряжения на реостате и катушке, а также сдвиг фаз между напряжением источника и напряжением на катушке, если U=220 В. Частота переменного тока f=50 Гц. Вычислить активную, реактивную и полную мощности катушки. Построить векторную диаграмму.

Решение:

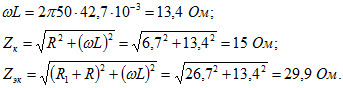
Ток в цепи
Разность фаз между напряжением и током определяют из выражения

Напряжения на реостате и катушке:

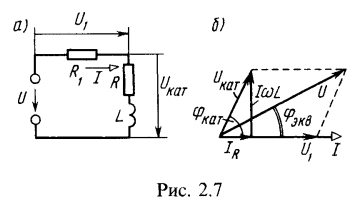
Сдвиг фаз между напряжением источника и напряжением на катушке найдется как разность фазовых углов (см. векторную диаграмму рис. 2.7, б):

Активная, реактивная и полная мощности катушки:

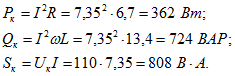
5. Для определения параметров эквивалентной схемы пассивного двухполюсника АВ (рис. 2.10, а) измерены напряжения , ток и мощность . Для определения характера эквивалентного реактивного сопротивления этого двухполюсника последовательно с ним включили конденсатор (рис. 2.10, б); в этом случае при том же приложенном напряжении приборы показали . Частота переменного тока f=50 Гц. Определить параметры эквивалентной схемы двухполюсника.

Решение:
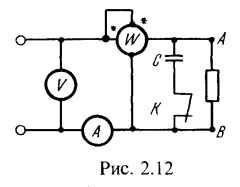
Параметры эквивалентной схемы двухполюсника по исходным данным (первый опыт)

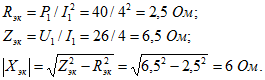
Из данных второго опыта найдем

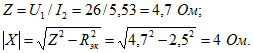
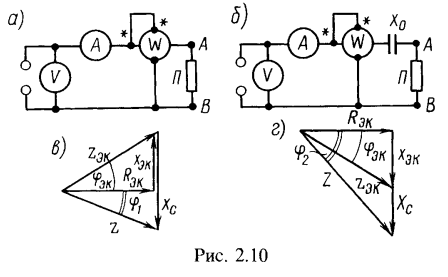
При неизменном напряжении, подключенном к цепи, и постоянном резистивном сопротивлении ток оказался больше тока . Введенное дополнительное емкостное сопротивление уменьшает общее реактивное сопротивление цепи. Это значит, что имеет индуктивный характер. Значение .
Неизвестное значение дополнительно введенного емкостного сопротивления можно определить следующим путем. Установлено, что , а так как характер полного реактивного сопротивления заранее неизвестен, то . Из данных второго опыта следует, что , отсюда получаем, что .
Укажем, что для определения характера эквивалентного реактивного сопротивления двухполюсника неизвестное значение дополнительно вводимого емкостного сопротивления должно быть меньше . Это можно видеть из рис. 2.10, в и г, на которых начерчены векторные диаграммы сопротивлений, соответствующие второму опыту. Для и при (рис. 2.10, в), а при (рис. 2.10, г). Если взять , то каждый из углов больше .
Если значение дополнительно вводимого сопротивления заранее известно, го оно может быть взято и более .

6. Приборы, подключенные к пассивному двухполюснику АВ (на рис. 2.12 контакт К разомкнут), показали . Для определения характера реактивного сопротивления двухполюсника параллельно ему был подключен конденсатор (контакт К замкнут), емкостное сопротивление которого , при этом приборы показали: . Определить эквивалентные параметры двухполюсника.

Решение:
Сопротивления последовательной схемы двухполюсника:

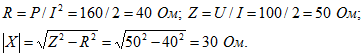
Параметры его параллельной схемы равны:

Проводимость конденсатора .
Параметры эквивалентной схемы, состоящей из двухполюсника и конденсатора:

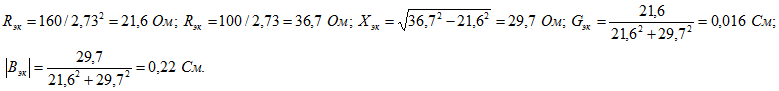
Так как , то реактивное сопротивление исследуемого двухполюсника имеет емкостный характер. Тог же результат вытекает и из следующих сображсний. Так как при том же напряжении ток после подключения конденсатора стал больше, чем до подключения, то общая проводимость цепи увеличилась. Это может быть в том случае, когда реактивная проводимость подключаемой ветви имеет тот же характер, что и заданная реактивная проводимость В двухполюсника, при условии, что .

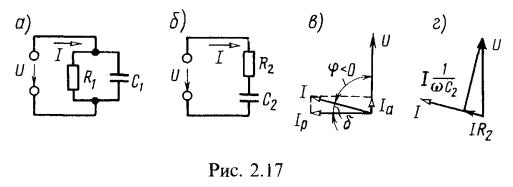
7. Для определения параметров конденсатора с потерями его подключили к источнику синусоидального напряжения U=19,5 В (f=50 кГц). При этом амперметр показал ток I=0,3 А, а ваттметр мощность Р=153 мВт. Определить двух схем рис. 2.17, а и б, эквивалентных конденсатору с потерями. Чему равны тангенс угла потерь указанного конденсатора и его добротность?

Решение:
Определим сдвиг фаз между напряжением U и током I:

Знак отрицателен, так как цепь состоит из резистивного сопротивления и емкости.
Из схемы рис. 2.17,а видно, что .
Найдем активную составляющую тока

Так как

то

Если реактивный ток

Для схемы рис. 2.17, б:

Отсюда

Угол потерь и его тангенс соответственно равны:

Для схем рис. 2.17, а и б даны соответствующие векторные диаграммы на рис. 2.17, в и г.
Добротность конденсатора

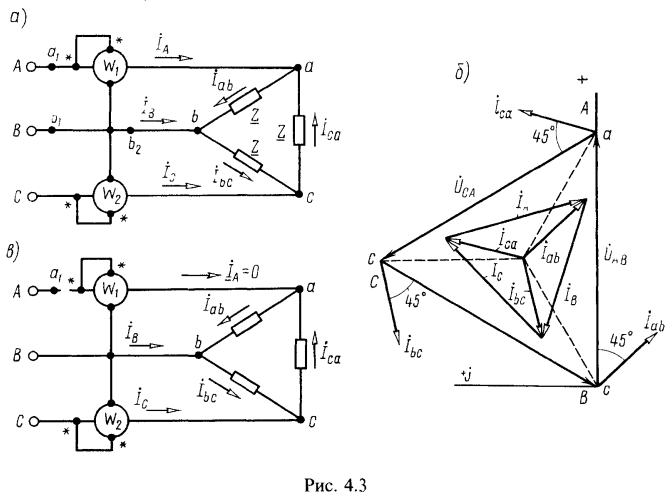
8. К трехфазной линии с симметричными линейными напряжениями подключен треугольником приемник, сопротивление каждой фазы которого (рис. 4.3, а). Найти токи в каждой фазе нагрузки и линии и показания каждого ваттметра. Найти те же величины в случае обрыва в точке .

Решение:
Задачу решим, пользуясь символическим методом. Примем, что комплекс напряжения действителен. Тогда комплексы линейных напряжений

Определим комплексы фазных и линейных токов:

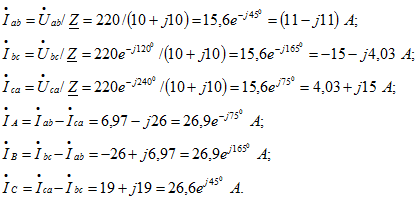
Найдем показания ваттметров:

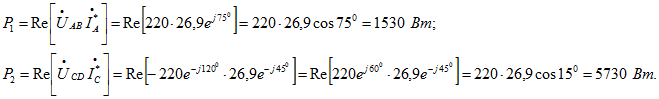
Активная мощность цепи
Проверка показывает, что
На рис. 4.3, б построена векторная диаграмма напряжений и токов.
Обрыв в точке (рис. 4.3, в). Токи в фазах нагрузки

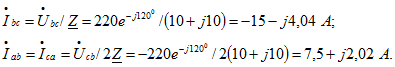
Вычислим линейные токи:

Определим показания ваттметров: