Трансформаторные подстанции высочайшего качества

1. Потенциальная энергия взаимодействия атомов в кристаллической решетке дается формулой , где n>1 (рис. 1). Первый член представляет силы притяжения, которые преобладают на больших расстояниях, второй член описывает силы отталкивания, преобладающие на малых расстояниях.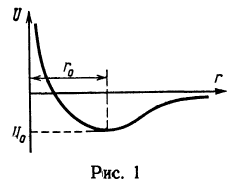
Найдите равновесное расстояние , глубину потенциальной ямы , частоту колебаний . Постройте потенциальную кривую для NaCl, найдя соответствующие атомные характеристики. Решетка NaCl кубическая, плотность каменной соли , энергия ее решетки 180 ккал/моль, а частота колебаний, определяемая по измерению показателя преломления, .

Решение. Минимум потенциальной энергии определяется условием . Отсюда следует, что . Потенциальную энергию вблизи положения равновесия можно представить в виде

Тогда Частота колебаний .
Расстояние может быть найдено по плотности. Поскольку атомный вес натрия равен 23, а хлора 35,5, то средний атомный вес равен (23+35,5)/2 = 29,25. Поэтому

где — масса протона. Так как для NaCl 180 ккал/моль соответствует Дж/ион, то имеем . Далее получаем . Поскольку, с другой стороны, , находим . Из соотношения получаем . Следовательно, потенциальная кривая для иона в соли NaCl может быть представлена в виде

Следует заметить, что обычно n берут равной 9 или 10, что лучше согласуется с термодинамическими данными о сжимаемости.

2. Исходя из потенциальной кривой для U, полученной в задаче 1., найти объемный коэффициент теплового расширения NaCl при Т=300К.

Решение. Тепловое расширение происходит вследствии того, что равновесное расстояние между атомами при повышении температуры возрастает. Для расчета возрастания необходимо принять во внимание ангармоничность колебаний. Имеем

Взяв в качестве U выражение (1) из 1., получаем

где, есть отклонение от точки , которое различно в разные стороны, что эквивалентно утверждению о смещении точки равновесия. По теореме о равнораспределении энергия колебаний равняется . Величины максимальных отклонений находим из условия, что вся кинетическая энергия превратилась в потенциальную, т. е. из условия

Отсюда получаем

Это означает, что средняя точка колебаний сместилась на . На ту же величину сместился и другой атом, т. е. расстояние увеличилось за счет тепловых колебаний при температуре 300 К на . Следовательно, коэффициент линейного расширения а равен

Экспериментальное значение . Разница в два раза объясняется грубостью модели и прикидочным значением используемых параметров.

3. Работа выхода у калия равна 2эВ, а у вольфрама — 4,54 эВ. Зарядами какого знака заряжаются калий и вольфрам при соприкосновении? Чему равна возникающая при этом разность потенциалов? Почему при разведении поверхностей соприкосновения на них не остается заряд?

Решение. Поскольку работа выхода у вольфрама больше, чем у калия, при контакте вольфрам заряжается отрицательно. Контактная разность потенциалов равна 4,54—2 = 2,54 В. Вольфрам и калий — проводники. Если бы можно было их поверхности соприкосновения развести одновременно во всех точках, то заряды на поверхности остались бы и тела зарядились, как это случается у диэлектриков. Практически же поверхности разводятся не одновременно во всех точках, а в некоторой последовательности. Площадь его последнего соприкасающегося участка стремится к нулю и к нулю стремится величина находящегося на нем заряда.

4. На поверхность калия падает фотон с длиной волны 0,40 мкм. Этот фотон поглощается внутри материала и передает всю свою энергию некоторому электрону, который устремляется к поверхности, преодолевает силы, удерживающие его в металле (фотоэффект) и покидает металл. Чему равна скорость электрона вне металла? Работа выхода из калия А=2 эВ.

Решение. Записываем закон сохранения энергии для процесса (уравнение Эйнштейна):

где — частота падающего фотона. Отсюда.

так как

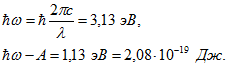
5. Оценить порядок величины энергии Ферми для меди.

Решение. В меди вне замкнутой оболочки содержится один электрон, который обобществляется и входит в число свободных электронов металла. Таким образом, для грубой оценки можно считать, что число свободных электронов у меди равно числу атомов. Энергия Ферми связана с числом свободных электронов N и объемом V, занимаемым металлом, соотношением

У меди удельный вес около , а атомный вес 63,5. Следовательно, ее молярный объем, в котором содержится атомов (и такое же число свободных электронов), равен . Подставляя эти значения в формулу для энергии Ферми, находим

6. Оценить величину внутренней контактной разности потенциалов между медью и калием при температуре 27° С.

Решение. Внутренняя контактная разность потенциалов равна

где — концентрации свободных электронов. Медь и калий входят в группу одновалентных элементов, у которых вне замкнутой оболочки находится один электрон, который обобществляется. Следовательно, на один атом приходится один свободный электрон. Поэтому для отношения концентраций свободных электронов в них можно написать

где — удельные и атомные веса соответствующих металлов. Для меди ; для калия . Отсюда