Электрическая емкость (страница 2)
1. К пластинам плоского конденсатора приложено напряжение U = 220 в.
Определить напряженность электрического поля Е между пластинами в средней его области, если расстояние между пластинами d=1 мм. Чему равна сила F, действующая в этой области поля на частицу с зарядом ![]() ?
?
Решение:
В средней области пространства между пластинами плоского конденсатора электрическое поле можно считать однородным. Линии напряженности электрического поля начинаются на поверхности положительно заряженной пластины и кончаются на поверхности отрицательно заряженной пластины. Эти линии перпендикулярны к пластинам. Поэтому расстояние между пластинами равно длине линии напряженности электрического поля. Следовательно, электрическое напряжение между пластинами, поделенное на расстояние между ними, равно напряженности электрического поля:
![]()
где расстояние d измерено в метрах. На частицу, обладающую электрическим зарядом ![]() , в этом поле действует сила
, в этом поле действует сила![]()
Единица измерения силы дж/м называется ньютоном (сокращенно н).
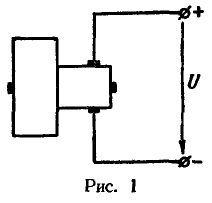
2. Напряжение между разомкнутыми зажимами генератора равно 115 в (рис. 1).
Определить потенциалы зажимов при: а) заземлении зажима «плюс»; б) заземлении зажима «минус».
Решение:
Электрическое напряжение U между зажимами «плюс» и «минус» генератора равно разности потенциалов этих зажимов: ![]() . В первом случае заземлен зажим «плюс», следовательно,
. В первом случае заземлен зажим «плюс», следовательно, ![]() . Подставив числовые значения, получим
. Подставив числовые значения, получим
![]()
откуда ![]()
Во втором случае заземлен зажим «минус», следовательно, ![]() . Подставив числовые значения, будем иметь
. Подставив числовые значения, будем иметь
![]()
откуда ![]()
На основании решения задачи можно видеть, что определенной величиной является электрическое напряжение. Оно не изменяется при изменении потенциалов всех точек поля на одну и ту же величину одновременно. В то же время потенциалы в отдельных точках электрического поля могут изменяться в зависимости от заземления той или иной точки.
3. Определить необходимую толщину слоя слюды между пластинами плоского конденсатора, если его номинальное напряжение ![]() должно быть в 4 раза меньше пробивного напряжения
должно быть в 4 раза меньше пробивного напряжения ![]() . Пробивная напряженность слюды
. Пробивная напряженность слюды ![]() . Какой толщины потребуется электрокартон (для него
. Какой толщины потребуется электрокартон (для него ![]() ), если его применить вместо слюды?
), если его применить вместо слюды?
Решение:
Пробивное напряжение
![]()
Принимая электрическое поле плоского конденсатора однородным, получим искомую толщину слоя слюды:
![]()
Так как пробивное напряжение равно 24 кв, то искомая толщина электрокартона
![]()
Отношение толщин связано с отношением напряженности следующим образом:
![]()
Следовательно, необходимые толщины диэлектрика обратно пропорциональны пробивным напряженностям.
4. Конденсатор емкостью С=1 мкф присоединен к сети с постоянным напряжением U=220 в.
Определить электрический заряд ![]() пластины, соединенной с положительным полюсом сети. Каким был бы электрический заряд, если бы напряжение сети было вдвое меньше?
пластины, соединенной с положительным полюсом сети. Каким был бы электрический заряд, если бы напряжение сети было вдвое меньше?
Решение:
Электрический заряд
![]()
где вследствие подстановки емкости С, измеренной в микрофарадах, электрический заряд ![]() измерен в микрокулонах.
измерен в микрокулонах.
Емкость С конденсатора — постоянная величина, если диэлектрические свойства изолятора между пластинами не зависят от напряжения U, приложенного к пластинам конденсатора. Такая электрическая емкость называется линейной.
Когда конденсатор с линейной емкостью присоединяется к сети, имеющей вдвое меньшее напряжение, электрический заряд будет также вдвое меньше:
![]()
Поэтому правильный выбор емкости конденсатора обеспечивает необходимой величины заряд в случае включения конденсатора на номинальное напряжение.
5. Плоский конденсатор имеет емкость С = 20 пф.
Какими следует выбрать толщину диэлектрика из стекла ![]() и площадь пластин, если конденсатор должен работать при номинальном напряжении
и площадь пластин, если конденсатор должен работать при номинальном напряжении ![]() , имея четырехкратный запас прочности?
, имея четырехкратный запас прочности?
Решение:
Пробивное напряжение при четырехкратном запасе прочности в 4 раза больше номинального напряжения:
![]()
Искомая толщина стекла
![]()
Из формулы емкости плоского конденсатора
![]()
определяем площадь пластины. В этой формуле величины измерены:![]()
Подставим в нее числовые значения:
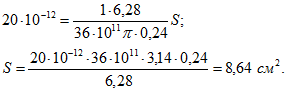
При меньших значениях ![]() и больших значениях d площадь пластины конденсатора должна быть больше.
и больших значениях d площадь пластины конденсатора должна быть больше.
6. Емкость конденсатора переменной емкости можно плавно изменять от 10 до 200 пф.
Какие границы изменения емкости можно получить, если присоединить к этому конденсатору такой же второй конденсатор?
Решение:
Присоединение второго конденсатора может быть последовательным и параллельным. Если второй конденсатор присоединен параллельно первому, то их эквивалентная емкость равна сумме емкостей отдельных конденсаторов.
Наибольшая емкость составит:
![]()
Если второй конденсатор присоединить последовательно к первому, то обратная величина эквивалентной емкости будет равна сумме величин, обратных емкостям отдельных конденсаторов. Поэтому наименьшая емкость определится так:
![]()
откуда
![]()
Таким образом, емкость изменяется от 5 до 400 пф.
Последовательное присоединение второго конденсатора уменьшило минимальную емкость, а параллельное присоединение второго конденсатора увеличило максимальную емкость.
При последовательном соединении двух одинаковых конденсаторов схему можно включать на напряжение в два раза большее, чем при параллельном соединении.