Закон Ома (страница 1)
Применение закона Ома к расчету линейных электрических цепей постоянного тока
1. Найти ток ветви (рисунок 3), если: U=10 В, Е=20 В, R=5 Ом.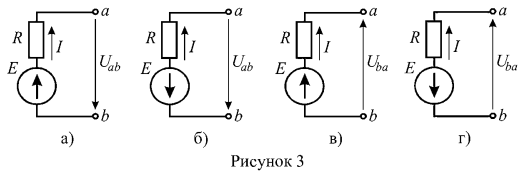
Решение:
Так как все схемы рисунка 3 представляют собой активные ветви, то для определения токов в них используем закон Ома обобщенный закон Ома. Рассмотрим рисунок 3 а: направление ЭДС совпадает с произвольно выбранным условно положительным направлением тока, следовательно, в формуле обобщенного закона Ома величина ЭДС учитывается со знаком «плюс». Направление напряжения ![]() не совпадает с направлением тока, и в формуле обобщенного закона Ома величина напряжения учитывается со знаком «минус»;
не совпадает с направлением тока, и в формуле обобщенного закона Ома величина напряжения учитывается со знаком «минус»;
![]()
Аналогично определяются токи в схемах б, в, г рисунка 3:
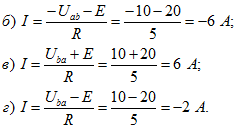
2. Найти напряжение между зажимами нетвей (рисунок 4).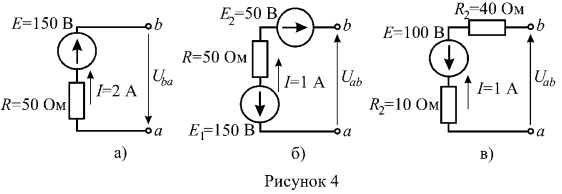
Решение:
Участок цепи, изображенный на рисунке 4 а содержит источник ЭДС, т.е. является активным, поэтому воспользуемся обобщенным законом Ома:
![]()
откуда выразим напряжение на зажимах:
![]()
Аналогично определяются напряжения на зажимах участков, изображенных на рисунках 4 б и 4 в.
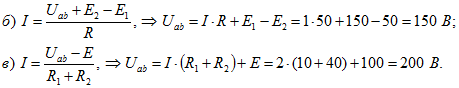
3. Определить неизвестные потенциалы точек участка цени (рисунок 5).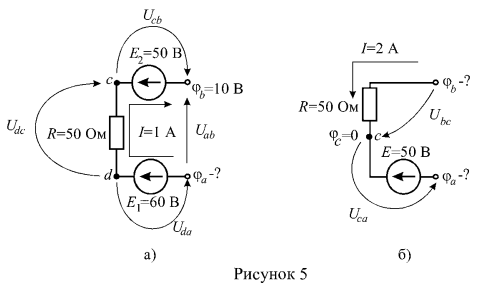
Решение:
Для схемы рисунка 5 а запишем обобщенный закон Ома:
![]()
откуда выразим напряжение на зажимах ветви:
![]()
Если представить напряжение ![]() как разность потенциалов:
как разность потенциалов:
![]()
тогда при известных параметрах цепи, токе и потенциале ![]() определим потенциал
определим потенциал ![]() :
:
![]()
Эту же задачу можно решить другим способом. Напряжение на зажимах источника ЭДС ![]() , без учета внутреннего сопротивления источника, по величине равно
, без учета внутреннего сопротивления источника, по величине равно ![]() и направлено от точки с большим потенциалом (точка С) к точке с меньшим потенциалом (точка b):
и направлено от точки с большим потенциалом (точка С) к точке с меньшим потенциалом (точка b):
![]()
и тогда, зная потенциал ![]() , определим потенциал точки С:
, определим потенциал точки С:
![]()
Потенциал точки d больше потенциала точки С на величину падения напряжения на сопротивлении R:
![]()
тогда
![]()
Потенциал точки а определяем с учетом направления напряжения ![]() на зажимах источника ЭДС
на зажимах источника ЭДС ![]() . Напряжение
. Напряжение ![]() направлено от точки с большим потенциалом (точка d) к точке с меньшим потенциалом (точка а):
направлено от точки с большим потенциалом (точка d) к точке с меньшим потенциалом (точка а):
![]()
откуда следует, что
![]()
или
![]()
Рассмотрим решение задачи для схемы рисунка 5 б. При известном потенциале точки С, параметрах элементов и токе, определим потенциалы крайних точек участка цепи ![]() . Напряжение на участке b — с, выраженное через разность потенциалов, определим по закону Ома:
. Напряжение на участке b — с, выраженное через разность потенциалов, определим по закону Ома:
![]()
откуда следует
![]()
Напряжение на участке с — а, равное по величине Е, направлено от точки с большим потенциалом к точке с меньшим потенциалом:
![]()
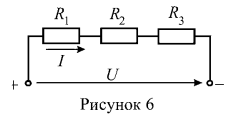
4. В цепи (рисунок 6) известны величины сопротивлений резистивных элементов: ![]() , входное напряжение U=100 В и мощность, выделяемая на резистивном элементе с сопротивлением
, входное напряжение U=100 В и мощность, выделяемая на резистивном элементе с сопротивлением ![]() . Определить величину сопротивления резистора
. Определить величину сопротивления резистора ![]() .
.
 Решение:
Решение:
Согласно закону Джоуля-Ленца, мощность на резистивном элементе определяется:
![]()
или, согласно закону Ома:
![]()
По известному значению мощности на резистивном элементе ![]() и величине сопротивления этого элемента определим ток в ветви:
и величине сопротивления этого элемента определим ток в ветви:
![]()
По закону Ома напряжение на зажимах определится:
![]()
тогда величина сопротивления резистивного элемента:
![]()
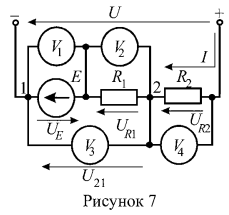
5. Определить показания вольтметров цепи (рисунок 7), если ![]() .
.
 Решение:
Решение:
Ток в цепи определим по закону Ома:
![]()
Вольтметр ![]() показывает напряжение на источнике ЭДС Е:
показывает напряжение на источнике ЭДС Е:
![]()
Вольтметры ![]() показывают величину падения напряжения на резистивных элементах
показывают величину падения напряжения на резистивных элементах ![]() :
:
![]()
Вольтметр ![]() , показывает напряжение на участке 2 — 1
, показывает напряжение на участке 2 — 1 ![]() , которое определим как алгебраическую сумма напряжений
, которое определим как алгебраическую сумма напряжений ![]() :
:
![]()
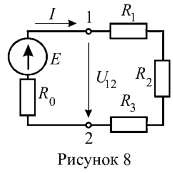
6. Ток симметричной цепи (рисунок 8) ![]() , внутреннее сопротивлении источника ЭДС
, внутреннее сопротивлении источника ЭДС ![]() . Определить ЭДС Е и мощность источника энергии.
. Определить ЭДС Е и мощность источника энергии.
 Решение:
Решение:
Напряжение на зажимах 1 — 2 определим по закону Ома для пассивной ветви:
![]()
Величину ЭДС источника энергии определим из выражения закона Ома для активной ветви:
![]()
Мощность, развиваемая источником энергии, определится:
![]()