Синхронные машины (страница 1)
Электромагнитные процессы в синхронной машине при холостом ходе
1. Условие задачи отражает важные соотношения, характеризующие форму кривой напряжения и поля возбуждения при холостом ходе синхронной машины. Это позволяет представить взаимосвязь между системой коэффициентов, определяющих форму напряжения и магнитного поля, и оценить порядок их числовых значений.
Числовые значения величин: 
Определить: 
, а также новое значение р.
Решение:
Покажем схематично (рис. 9) синхронную машину, имеющую на роторе неявнополюсную распределенную двухполюсную обмотку возбуждения с длиной обмотанной части полюса b. Заданная по условию относительная длина обмотанной части полюса 
. Распределение вдоль расточки статора магнитодвижущей силы, образуемой этой обмоткой при протекании в ней тока возбуждения, представим ступенчатой кривой. При этом на необмотанной части полюса (большой зуб) МДС обмотки неизменна.
Индукция в зазоре 
. Поэтому кривая индукции повторяет по форме кривую МДС. Она также ступенчата с максимальным значением индукции на оси полюса:
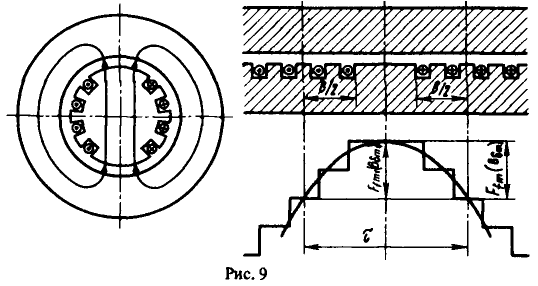
При разложении ступенчато распределенной индукции в гармонический ряд первую гармоническую индукцию 
можно определить с помощью коэффициента формы поля возбуждения 
. Для рассматриваемой неявнополюсной машины
Соответственно 
Полный поток взаимной индукции
где расчетный коэффициент полюсного перекрытия 
; полюсное деление 
. Откуда
Магнитный поток взаимной индукции, соответствующий первой гармонической индукции,
Коэффициент потока возбуждения
Коэффициент формы ЭДС 
определим по формуле
Приравнивая выражения для полного потока и потока по первой гармонической 
, получаем
откуда новое значение относительной длины обмотанной части полюса
Ответ: 
Электромагнитные процессы в синхронной машине при нагрузке
2. Задача относится к исследованию электромагнитных процессов явнополюсной синхронной машины при нагрузке и связана с учетом влияния поля якоря на поле возбуждения при насыщении. Решение задачи проводится графоаналитически с применением векторных диаграмм.
Числовые значения величин: 
Нормальные характеристики намагничивания приведены в таблице 1.
Определить: 
Решение:
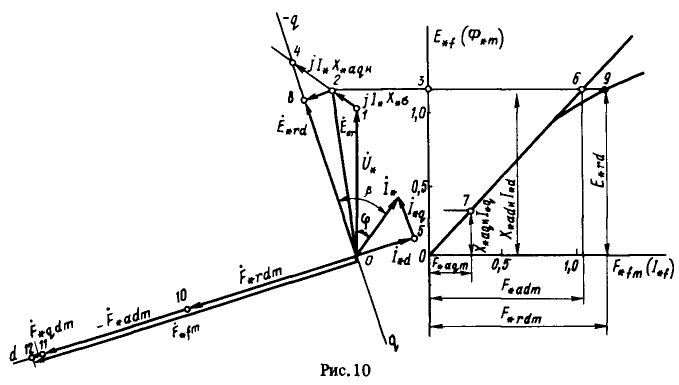
Необходимо выбрать масштаб для построения характеристик намагничивания. Выбор масштаба ориентировочно проводится из условия размещения кривых намагничивания в правой верхней части листа выбранного формата (рис. 10). В нашем случае при формате 330×200 мм 
.
Определим ток возбуждения без учета изменения потока рассеяния обмотки возбуждения. По данным таблице 1 в выбранном масштабе строим основную характеристику холостого хода 
. В масштабе 
откладываем вектор напряжения 
и под углом 
строим вектор тока 
в произвольном масштабе (здесь 
).
| ТАБЛИЦА 1. ДАННЫЕ НОРМАЛЬНЫХ ХАРАКТЕРИСТИК ХОЛОСТОГО ХОДА И НАМАГНИЧИВАНИЯ НЕЯВНОПОЛЮСНЫХ СИНХРОННЫХ МАШИН | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
 | 0 | 0,1 | 0,25 | 0,5 | 0,75 | 1 | 1,5 | 2 | 2,5 | 3 | 3,5 |
 | 0 | 0,116 | 0,29 | 0,58 | 0,83 | 1 | 1,2 | 1,2 | 1,33 | 1,46 | 1,51 |
 | 0 | 0,116 | 0,29 | 0,58 | 0,84 | 1,02 | 1,28 | 1,28 | 1,47 | — | — |
 | 0 | 0,116 | 0,29 | 0,58 | 0,87 | 1,16 | 1,74 | 2,32 | — | — | — |
 | 0 | 0,005 | 0,0115 | 0,023 | 0,034 | 0,046 | 0,69 | 0,091 | 0,114 | 0,137 | 0,16 |
 | 0 | 1,22 | 1,34 | 1,42 | 1,48 | 1,54 | 1,63 | — | — | — | — |
Чтобы определить результирующую ЭДС взаимной индукции 
, от конца вектора 
отложим вектор 
, длина которого 
; в выбранном масштабе 0,2:0,2=1 см соответствует напряжению 
в относительных единицах. Измерив длину отрезка 
, получим 
.
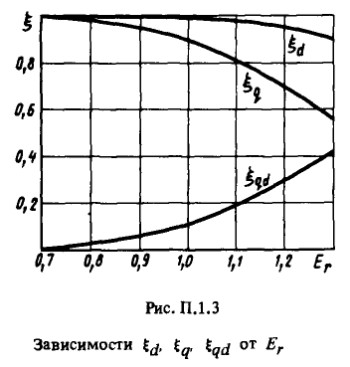
По величине 
с помощью кривых (рисунок П 1.3) определим коэффициенты 
и вычислим значения главных индуктивных сопротивлений с учетом насыщения:
К вектору 
прибавим вектор 
, длина которого в масштабе напряжения 
. Конец комплекса 
определяет направление вектора 
(угол 
) и направление оси (-q) машины. Ось d опережает ось (-q) на угол 
.
Определим продольную и поперечную составляющие тока, раскладывая ток 
по направлениям осей d и q: 
.
По полученным значениям составляющих тока определим соответствующие им ЭДС:
По продолжению прямолинейного участка характеристики холостого хода находим эквивалентные МДС возбуждения: 
.
Рассчитаем МДС 
эквивалентную размагничивающему влиянию поперечной МДС на продольное поле: 
.
Чтобы определить результирующую МДС по продольной оси 
, спроектируем 
на направление оси (-q). Получим комплекс 
. По величине ЭДС 
с помощью характеристики холостого хода находим величину 
.
Полная МДС возбуждения
В масштабе 
эти составляющие МДС на диаграмме представляются отрезками 1,2/0,2 = 6 см, 1,04/0,2 = 5,2 см и 0,064/0,2 = = 0,32 см соответственно.
Искомый ток возбуждения в относительных единицах равен полной МДС возбуждения
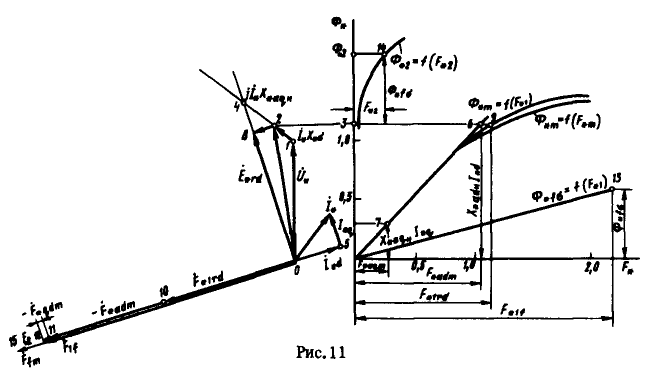
Определим ток возбуждения при нагрузке с учетом изменения потока рассеяния обмотки возбуждения. Для этого построим частичные характеристики намагничивания по данным таблицы 2 (рис. 11). Выполним расчеты и построения, аналогичные предыдущим. Отличие состоит в определении результирующей МДС по продольной оси.
| ТАБЛИЦА 2. ДАННЫЕ НОРМАЛЬНЫХ ХАРАКТЕРИСТИК ХОЛОСТОГО ХОДА И НАМАГНИЧИВАНИЯ ЯВНОПОЛЮСНЫХ СИНХРОННЫХ МАШИН | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
 | 0 | 0,1 | 0,2 | 0,3 | 0,5 | 0,75 | 1 | 1,25 | 1,5 | 1,75 | 2 |
 | 0 | 0,106 | 0,212 | 0,318 | 0,53 | 0,8 | 1 | 1,225 | 1,23 | 1,26 | 1,3 |
 | 0 | 0,106 | 0,212 | 0,318 | 0,53 | 0,8 | 1 | 1,2 | 1,28 | 1,31 | 1,35 |
 | 0 | 0,106 | 0,212 | 0,318 | 0,53 | 0,8 | 1,06 | 1,325 | 1,59 | 1,855 | 2,12 |
 | 0 | 0,026 | 0,052 | 0,078 | 0,131 | 0,196 | 0,262 | 0,328 | 0,393 | 0,458 | 0,525 |
 | 0 | 1,5 | 1,675 | 1,75 | - | - | - | - | - | - | - |
С помощью частичной характеристики 
по величине 
сначала определим значение 
без учета магнитного напряжения ротора, 
, а затем найдем МДС возбуждения 
без учета магнитного напряжения ротора:
По частичной характеристике 
определим поток рассеяния 
, соответствующий МДС 
.
Поток в полюсе
По частичной характеристике 
найдем соответствующее магнитное напряжение ротора
.
Полную МДС возбуждения и искомый ток возбуждения в относительных единицах определим как сумму
Как видно, МДС возбуждения, определенная этим способом больше МДС, найденной без учета изменения потока рассеяния обмотки возбуждения на величину 2,514 — 2,3 = 0,214 о.е.
Ответ: 
Характеристики синхронного генератора при автономной нагрузке
3. Задача относится к определению и графическим построениям характеристик синхронного генератора при автономной нагрузке. Регулировочная характеристика генератора — это зависимость тока возбуждения от тока якоря 
при постоянных напряжении, угловой скорости вращения в угле нагрузки 
. Без учета насыщения искомую характеристику можно получить аналитически, для учета насыщения необходимы графические построения с использованием характеристики намагничивания, диаграммы напряжений и МДС.
Числовые значения величин: 
Характеристика холостого хода определяется по данным из таблицы 1.
Определить 
с учетом и без учета насыщения.
Решение:
Регулировочную характеристику без учета насыщения определим с помощью выражения
которое в относительных единицах для 
запишется в виде
Вместо ЭДС 
введем ток возбуждения 
, определяемый по спрямленной нормальной характеристике холостого хода, построенной по данным таблицы 1 в масштабе 
(рис. 12).
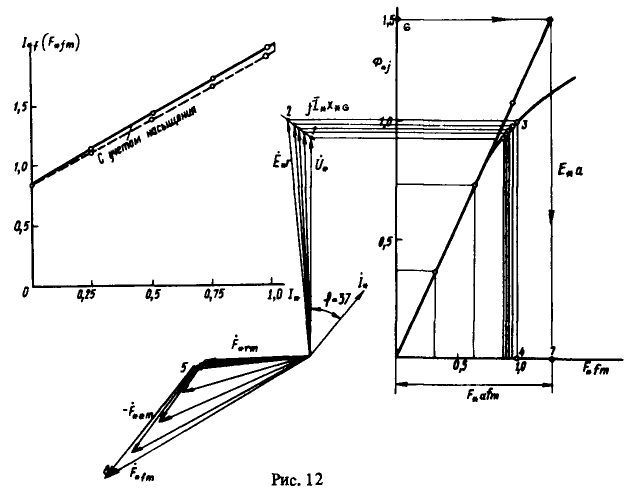
Индуктивное сопротивление якоря 
. Для заданного значения 
аналитическое выражение регулировочной характеристики имеет вид
Задаваясь пятью значениями токов 
в диапазоне от 0 до 1, найдем соответствующие значения тока возбуждения:
| Значения тока | |||||
|---|---|---|---|---|---|
| 0 | 0,25 | 0,5 | 0,75 | 1 |
| 0,862 | 1,1 | 1,376 | 2 | 2 |
Для учета насыщения при построении регулировочной характеристики воспользуемся диаграммой напряжения и МДС. При этом для правильной оценки влияния насыщения примем, что ток возбуждения в режиме холостого хода 
одинаков для обоих случаев, 
.
В выбранном масштабе 
построим комплекс напряжения 
, соответствующий 
, и под углом 
— вектор тока 
в масштабе 
.
Для тока 
построим комплекс 
в масштабе напряжения 
и получим вектор результирующей ЭДС 
.
С помощью основной характеристики намагничивания по значению 
определим величину МДС, 
(рис. 12), для чего отложим на диаграмме комплекс МДС 
опережающий 
на угол 
.
По заданному значению главного индуктивного сопротивления 
определим ЭДС взаимной индукции 
и с помощью спрямленной характеристики холостого хода найдем значение эквивалентной МДС возбуждения 
.
Имея в виду, что МДС 
совпадает по фазе с током 
, a 
, определим графически относительную величину МДС возбуждения 
и равный ей по величине в относительных единицах ток возбуждения 
.
Повторив указанные выше действия для значения токов 
, получим пять точек регулировочной характеристики:
| Точки | |||||
|---|---|---|---|---|---|
| 0 | 0,25 | 0,5 | 0,75 | 1 |
 | 0,862 | 1,14 | 1,46 | 1,76 | 2,1 |
| 0,862 | 1,1 | 1,38 | 1,67 | 1,99 |
Третья строка соответствует точкам регулировочной характеристики, определенной без учета насыщения.
Как видно, регулировочные характеристики, построенные с учетом насыщения, мало отличаются от характеристик, рассчитанных без учета насыщения.
Ответ: см. регулировочные характеристики.