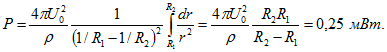Постоянный электрический ток

1. В цепи, изображенной на рис. 34, найти токи через каждую ветвь, если ЭДС источников тока равны а сопротивления — . Внутренним сопротивлением пренебречь.

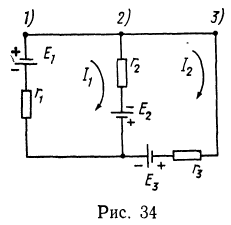Решение. Составляем уравнения для контурных токов (рис. 34):

Подставляя числовые значения, получим

Решаем систему (1′) методом определителей Крамера

где

Подставляя значения определителей в (2), получим

Находим физические токи.
В 1-й ветви физический и контурный токи совпадают:

Знак минус означает, что реально ток течет в направлении, противоположном выбранному. Во 2-й ветви физический ток равен

В 3-й ветви

2. Определить сопротивление изоляции на один погонный метр длины провода диаметром d=2 мм, если диаметр наружной проводящей оболочки равен D=4 мм, а удельное сопротивление фарфоровой изоляции равно (рис. 35).

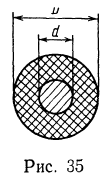Решение. В цилиндрической системе координат закон Ома в дифференциальной форме имеет вид (проекция на радиус-вектор)

Электрическое поле Е выразим через потенциал

где — напряжение между проводом и наружной оболочкой изоляции.
Из (1) и (2) найдем, что

Полный ток, отнесенный к длине провода , будет

Так как согласно закону Ома сила тока пропорциональна напряжению, то сопротивление изоляции на единицу длины провода равно

3. Определить количество энергии, поглощаемой в единицу времени веществом с удельным сопротивлением , которое заполняет пространство между двумя сферическими оболочками с радиусами , между которыми поддерживается разность потенциалов .