Трансформаторные подстанции высочайшего качества

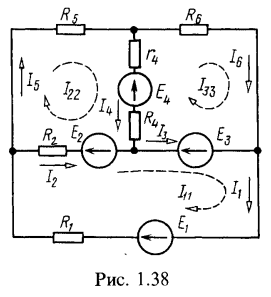
1. Методом контурных токов найти токи в цепи, схема которой изображена на рис. 1.38. Дано:

Решение:
Выберем направления контурных токов, которые обозначим через .
Составим систему уравнений для контуров:

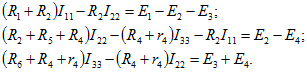
После подстановки числовых значений имеем:

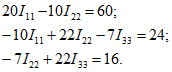
Решив эту систему уравнений, найдем контурные токи: , а затем — истинные токи во всех ветвях.
В ветви, где действует ЭДС , истинный ток имеет направление контурного тока и равен .
В ветви с сопротивлением истинный ток имеет направление контурного тока и равен .
В ветви с сопротивлением истинный ток получится от наложения контурных токов и будет иметь направление большего контурного тока .
В ветвях с сопротивлением истинный ток получится от наложения контурных токов и будет иметь направление контурного тока .
В ветви, где действует ЭДС , истинный ток получится от наложения контурных токов и будет иметь направление тока .
Для упражнения рекомендуем составить самостоятельно уравнения контурных токов в матричной форме.

2. Цепь (рис. 1.39) содержит источник тока , источник ЭДС и резисторы, сопротивления которых . Вычислить все токи методом контурных токов. Проверить баланс мощностей.

Решение:
Схема содержит шесть ветвей , четыре узла , один источник тока . Число независимых уравнений, составляемых по методу контурных токов, равно двум . Зададимся направлениями контурных токов , как показано на рис. 1.39. Там же нанесен известный контурный ток источника тока J. Составим систему уравнений для первого и второго контуров: .
Подставляя числовые значения, имеем .
Решая эти уравнения, найдем контурные токи: .
Искомые токи: .
Баланс мощностей: .
Подставляя числовые значения, получим тождество 11,2 Вт= 11,2 Вт.