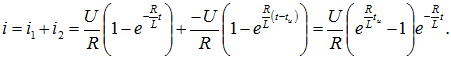Трансформаторные подстанции высочайшего качества

1. Рассчитать импульсные характеристики цепи (см. рис. 8.38) при воздействии на вход цепи источника ЭДС, полагая, что реакцией является: а) ток в неразветвленной части цепи; б) напряжение на резистивном элементе.

Решение:
Переходные характеристики цепи определены в задаче 1 предыдущего раздела: . Для определения импульсных характеристик цепи используем формулу:

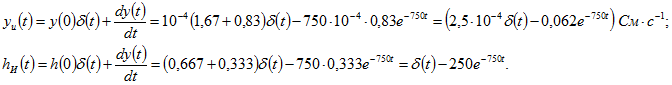
2. Цепь, состоящая из последовательно соединенных R=50 Ом и L=2,5 Гн, включается под действие напряжения . Найти ток в цепи и построить его кривую.

Решение:
Составляем дифференциальное уравнение по второму закону Кирхгофа:

Решение его

где — общий интеграл уравнения (8.1) без правой части, — частное решение уравнения (8.1).
Найдем . Как известно из курса математики, частное решение рассматриваемого линейного дифференциального уравнения определяется в форме показательной функции:

Подставляя это значение в (8.1), получим , откуда . Подставляя значение В в (8.3), получим

Переходный ток i [см. формулу (8.2)]

Для определения постоянной интегрирования А используем начальное условие :

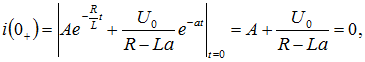
отсюда

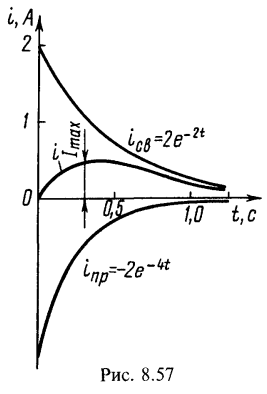
Таким образом,

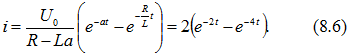
Кривая тока изображена на рис. 8.57.
Ток имеет максимум, найдем его

Приравнивая эту производную нулю, получим момент времени , при котором значение тока максимально

отсюда
Подставив это значение в формулу (8.6), найдем

3. Цепь, состоящая из последовательно соединенных R и L, включается на прямоугольный импульс напряжения U, действующий в течение времени (рис. 8.58, а). Найти выражение тока i и напряжение на индуктивной катушке в зависимости от времени. Построить кривые .

Решение:
а. Классический способ. Для интервала времени от t=0 до ток определяется так же, как и при включении той же цепи на постоянное напряжение U:

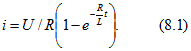
Напряжение на индуктивной катушке

При воздействие на цепь отсутствует, поэтому ток содержит только свободную составляющую. Она определяется энергией, накопленной в магнитном поле за время от 0 до . Итак, для , когда u=0, уравнение второго закона Кирхгофа . Его решение

Постоянную интегрирования А определим из того, что в момент ток в цепи, содержащей индуктивную катушку, не может измениться скачкообразно

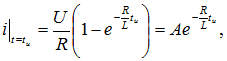
отсюда

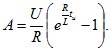
Подставляя значение А в уравнение (8.3), получим выражение тока при :

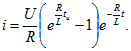
Выражение для напряжения на индуктивной катушке при :

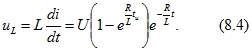
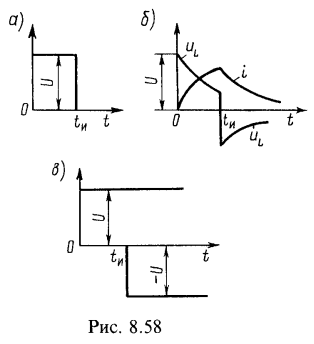
По уравнениям (8.1) (8.4) на рис. 8.58, б построены графики. Отметим, что в момент напряжение на индуктивной катушке изменяется скачком па величину, равную U. Скачок напряжения на индуктивности имеет место и при .

б. Принцип наложения. Прямоугольный импульс можно рассматривать как результат действия двух постоянных напряжений: напряжения U, включаемого в момент t=0 и действующего неограниченно долго, и отрицательного напряжения, равного — U, вступающего в действие в момент и также действующего неограниченно долго (рис. 8.58, в). Итак, для ток определяют, как и раньше, по формуле (8.1).
Для