Электростатика проводников и диэлектриков
ЭЛЕКТРОСТАТИКА ПРОВОДНИКОВ
1. Точечный заряд q находится на расстоянии а от заземленной проводящей плоскости. Определите Напряженность поля, созданного зарядом q и индуцированными на проводнике зарядами, распределение индуцированных зарядов и силу взаимодействии заряда q с проводящей плоскостью.
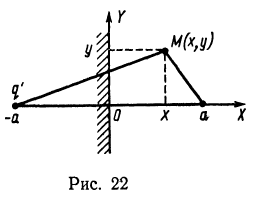 Решение. Изображением заряда q является заряд q‘=-q отстоящий на расстоянии а по другую сторону плоскости (рис. 22). По определению
Решение. Изображением заряда q является заряд q‘=-q отстоящий на расстоянии а по другую сторону плоскости (рис. 22). По определению
![]()
поэтому для компонент поля в плоскости r=0 получим
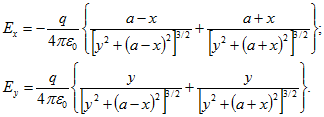
У поверхности проводника ![]() , поэтому
, поэтому
![]()
Сила взаимодействия равна
![]()
В произвольной точке проводящей плоскости координатой у, z
![]()
2. Если бы поверхностная плотность электрического заряда Земли была эквивалентна одному электрону на ![]() , то каков был бы потенциал Земли и какова была бы напряженность поля у ее поверхности?
, то каков был бы потенциал Земли и какова была бы напряженность поля у ее поверхности?
Решение. Рассмотривая Землю как сферу, заряженную с равномерной плотностью зарядом ![]() , получим для потенциала
, получим для потенциала
![]()
Напряженность поля найдем из условия ![]() . Тогда
. Тогда ![]() .
.
3. Чему равна сила, действующая на точечный заряд ![]() , расположенный на расстоянии а от поверхности заземленной проводящей сферы радиуса R. Чему равна поверхностная плотность индуцированных на сфере зарядов?
, расположенный на расстоянии а от поверхности заземленной проводящей сферы радиуса R. Чему равна поверхностная плотность индуцированных на сфере зарядов?
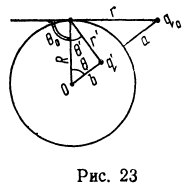 Решение. Так как поверхность сферы эквипотенциальна, то поле заряда
Решение. Так как поверхность сферы эквипотенциальна, то поле заряда ![]() и зарядов, индуцированных на поверхности сферы, эквивалентно лолю точечных зарядов q и q‘ причем
и зарядов, индуцированных на поверхности сферы, эквивалентно лолю точечных зарядов q и q‘ причем ![]() (рис. 23). Поэтому сила взаимодействия
(рис. 23). Поэтому сила взаимодействия
![]()
Поверхностную плотность индуцированных на сфере зарядов найдем из условия ![]() , где
, где ![]() — нормальная к поверхности сферы компонента поля
— нормальная к поверхности сферы компонента поля ![]() . Поэтому
. Поэтому
![]()
Учитывая, что
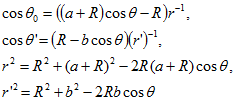
и что
![]()
получим
![]()
4. Два длинных провода диаметром d=1 мм, каждый расположены параллельно друг другу. Расстояние между их осями b=14 мм. Найдите взаимную емкость проводов ![]() , приходящуюся на единицу их длины.
, приходящуюся на единицу их длины.
Решение. Потенциал произвольной точки пространства, созданный заряженными разноименно проводниками, равен
![]()
Потенциалы самих проводников будут соответственно равны
![]()
По определению ![]() поэтому
поэтому ![]()
Для d= 1 мм, b=14 мм, получим ![]()
5. Плоский воздушный конденсатор емкостью С=1 МКФ зарядили до разности потенциалов ![]() и отключили от источника напряжения. Какую работу необходимо совершить, чтобы увеличить расстояние между пластинами конденсатора в пять раз? Какова будет после этого разность потенциалов между пластинами?
и отключили от источника напряжения. Какую работу необходимо совершить, чтобы увеличить расстояние между пластинами конденсатора в пять раз? Какова будет после этого разность потенциалов между пластинами?
Решение. По определению ![]() , где
, где ![]() . По условию
. По условию ![]() . Поэтому
. Поэтому
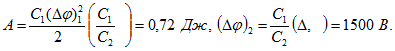
ЭЛЕКТРОСТАТИКА ДИЭЛЕКТРИКОВ
6. Однородный изотропный диэлектрик с восприимчивостью ![]() , имеющий форму шара, помещен в однородное внешнее поле
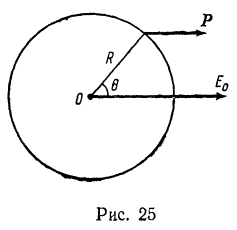
, имеющий форму шара, помещен в однородное внешнее поле ![]() . Определите поверхностную плотность наведенных на поверхности диэлектрика зарядов в точке, для которой радиус сферы образует с направлением поля угол
. Определите поверхностную плотность наведенных на поверхности диэлектрика зарядов в точке, для которой радиус сферы образует с направлением поля угол ![]() . Рассмотрите случай, когда сфера является проводником
. Рассмотрите случай, когда сфера является проводником ![]() (рис. 25).
(рис. 25).
 Решение. По определению
Решение. По определению ![]() . Так как
. Так как ![]() , то
, то ![]() . Для
. Для ![]() получим
получим ![]() .
.
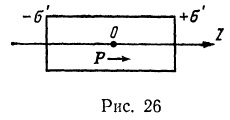
7. Сегнетоэлектрик, имеющий форму цилиндра радиуса R и высотой l, однородно поляризован (р = const) в направлении оси цилиндра вследствие спонтанной поляризации (рис. 26). Вычислите напряженность и потенциал электростатического поля, созданного поляризованным сегнетоэлектриком в точках на оси цилиндра, если его вектор поляризации равен Р. Для точек внутри цилиндра найдите также значение вектора электрического смещения.
Решение. Электрическое поле сегнетоэлектрика мы найдем, если будет известно распределение объемных (р’) и поверхностных (s‘) связанных электрических зарядов, которые определяются соотношениями![]()
 Для рассматриваемого сегнетоэлекприка в силу его однородной поляризации (P = const) р’ = 0, в то время как на торцах цилиндра
Для рассматриваемого сегнетоэлекприка в силу его однородной поляризации (P = const) р’ = 0, в то время как на торцах цилиндра ![]() (внешняя среда считается вакуумом и поэтому
(внешняя среда считается вакуумом и поэтому ![]() ).
).
Таким образом, мы пришли к задаче о поле двух заряженных дисков. Здесь мы приводим только результаты решения задачи, заменяя в них s на Р. При ![]()
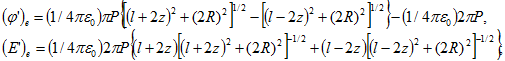
при ![]()
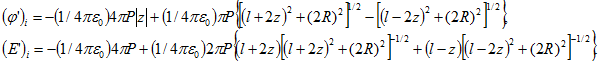
По определению ![]() . Поэтому для
. Поэтому для ![]()
![]()
и для ![]() (так как в этом случае Р=0)
(так как в этом случае Р=0)
![]()
т.е. вне сегнетоэлектрика вектор электрического смещения и вектор напряженности совпадают с точностью до постоянного множителя.
8. Тонкую пластинку из эбонита ![]() поместили в однородное электростатическое поле напряженностью
поместили в однородное электростатическое поле напряженностью ![]() так, что плоскость пластин, ки образуют с направлением поля угол в 60°. Найдите величину и направление векторов Р, Е и D в пластине.
так, что плоскость пластин, ки образуют с направлением поля угол в 60°. Найдите величину и направление векторов Р, Е и D в пластине.
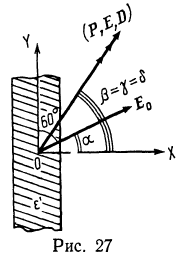 Решение. Векторы Р, Е и D имеют внутри пластинки одинаковое направление, образующее с плоскостью пластинки угол 30° (см. рис. 27). Учитывая что
Решение. Векторы Р, Е и D имеют внутри пластинки одинаковое направление, образующее с плоскостью пластинки угол 30° (см. рис. 27). Учитывая что ![]() , где
, где ![]() — факторы формы пластинки, и то, что
— факторы формы пластинки, и то, что ![]() , a,
, a, ![]() , найдем
, найдем
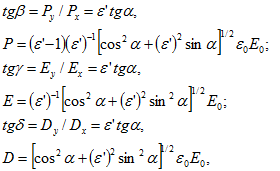
где ![]()
Таким образом,
![]()
9. Пространство между пластинами плоского конденсатора заполнено диэлектриком с проницаемостью ![]() , в котором в качестве примеси имеется малая сферическая частица диэлектрика с проницаемостью
, в котором в качестве примеси имеется малая сферическая частица диэлектрика с проницаемостью ![]() . Определите напряженность поля внутри этой частицы, если до заполнения диэлектриком напряженность поля между пластинами конденсатора была
. Определите напряженность поля внутри этой частицы, если до заполнения диэлектриком напряженность поля между пластинами конденсатора была ![]() .
.
Решение. Вычислим сначала поле внутри полости (сферической) диэлектрика (рис. 28):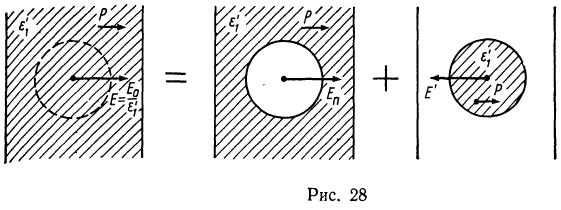
![]()
Поле внутри сферической частицы с проницаемостью ![]() равно (рис. 29)
равно (рис. 29)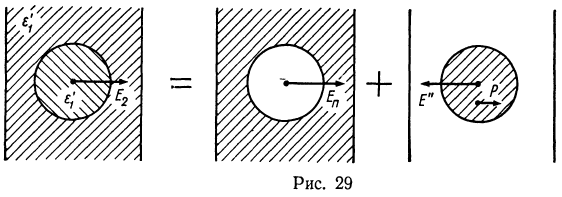
![]()
Е’ и Е» — деполяризующие поля в сферах с ![]() . Таким образам,
. Таким образам,
![]()
а) При ![]()
б) При ![]()
в) При ![]()
10. Очень тонкий цилиндрический стержень объемом V из однородного диэлектрика (изотропного) восприимчивостью ![]() находится в однородном поле
находится в однородном поле ![]() , образующем угол
, образующем угол ![]() с направлением оси стержня. Определить величину внешнего механического момента, который удерживает стержень в равновесии.
с направлением оси стержня. Определить величину внешнего механического момента, который удерживает стержень в равновесии.
Решение. В системе отсчета, выбранной так, что вектор ![]() лежит в плоскости XY, а ось X параллельна оси стержня, имеем
лежит в плоскости XY, а ось X параллельна оси стержня, имеем ![]() или
или ![]() , а также
, а также
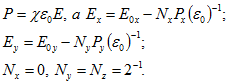
Поэтому
![]()
Примечание. Если ![]() , то
, то ![]() , если
, если ![]() , то
, то ![]() .
.